Árnyékokról már volt szó a shadow volume-os cikkben, amit pofátlan módon csak azért írtam, mert különben baromi hosszú lett volna ez a cikk. Sőt, külön arcátlanság volt ez tőlem, mert a játékok alig használnak shadow volume-ot (de a Doom 3 elég jól megcsinálta).

Ez a cikk egy népszerűbb technikáról, a shadow mapping-ról szól, de nem fogok minden módszert lefedni, mert jövőre se érnék a végére. Csak néhány érdekesebb shadowmap szűrési módszert hasonlítok össze (megjegyzem mindegyikhez található olyan játék, ami használja). Tökéletes megoldás sajnos nincs, mindegyiknek vannak kisebb-nagyobb hibái, amiknek a kiküszöböléséhez speciális meggondolások kellhetnek.

Ki gondolta volna, hogy ezt a technikát már 1978-ban kitalálta Lance Williams? Azért meglepő ez, mert ezek szerint még 2004-ben sem használták érdemben (dehogynem, csak nem valós időben). De mint tudjuk a legtöbb technikával ez így volt, teljesítmény- avagy látványbeli problémák miatt. Utóbbi ezzel is van bőven.

Na de először nézzük az alapkoncepciót: a fény szemszögéből kirajzolod a jelenet z értékeit egy textúrába (ez a shadowmap). Ez most egy elég általános megfogalmazás volt, de valójában a fényhez legközelebb eső árnyékvetőket (blocker) fogja így ez tartalmazni.

Rögtön az elején megemlíteném, hogy bár a korábbi cikkekben a fénytől való távolságot írtam ki, a helyes eljárás az, ha (linearizált) mélységet írsz a shadowmapbe. Ennek két oka is van, egyrészt a float precíziót optimálisan használja ki, másrészt a lenti technikák feltételezik, hogy a shadowmap értékei a [0, 1] intervallumban vannak. Sőt, egy még fontosabb dolog, hogy a fény projekciós mátrixa a lehető legjobban rá legyen igazítva a jelenetre (különösen a közeli és távoli vágósík). Némelyik módszer ugyanis érzékeny a [0, 1] intervallum kitöltöttségére is.

A shadowmap kirajzolásához gondolom nem kell különösebb kód, a projektív textúrázást pedig mindenki álmából felébresztve keni-vágja (ha esetleg nem, akkor ott a kód). Ezen információ birtokában a jelenet kamerával való kirajzolásakor eldönthető, hogy egy pixel árnyékban van-e vagy nem:

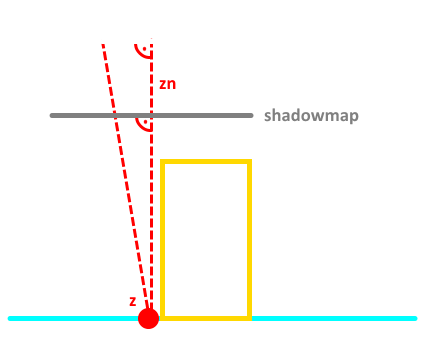
Amit ha végiggondolunk teljesen világos is, hiszen ha az adott pontot valami eltakarja, akkor ott árnyék van (z < d). Márpedig a shadowmap pont ezeket a takaró pontokat tartalmazza. A későbbiek érdekében ezt a fenti kódot formalizálni fogom a cikkhez felhasznált irodalmaknak megfelelően:

Legyen x ∈ R³ egy pont a térben amiről el akarjuk dönteni, hogy árnyékban van-e. Legyen p ∈ R² ennek a pontnak a levetítése light space-be (tehát amivel olvasni lehet a shadowmapből), és definiáljuk az árnyékolást (s) az alábbi f: R² → [0, 1] függvénnyel: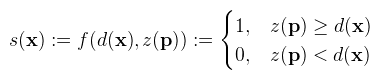


Ami tehát ugyanaz, mint a fenti kód. Az eddigiekhez képest most vastag betűvel jelölöm a vektorokat, hogy az irodalmakkal konzisztens legyen (gondolom ez senkit nem fog zavarni). A függvényt röviden f(d, z)-nek fogom írni. Ami egy fontos észrevétel, hogy ez az f könnyen átkonvertálható egy egyváltozós H függvénnyé úgy, hogy f(d, z) = H(z - d):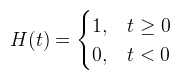


Itt egy picit eltértem az irodalmaktól, mert azok fordítva végzik el a kivonást, de én abban nem látom a logikát (kavarást viszont igen). A lényeg, hogy ez a H függvény (Heaviside step, magyarul "egységugrás") központi szerepet fog játszani a későbbiekben, ugyanis ezt szeretnénk majd közelíteni olyan függvényekkel, amikben z (d-től) független tagként szerepel (ezáltal szűréssel elsimítani a recés árnyékot).

Ha a fenti kódot valaki megcsinálja, akkor rövid időn belül fel fog tűnni, hogy az árnyék széle nagyon pixeles. Ez a perspektív megjelenítésnek egy hátránya, mivel a shadowmap world space-ben terül szét valami felületen, egy shadowmap texelhez több képernyőpixel tartozhat. A nagyobbik probléma, hogy egyszerűen nem lehet ezt elsimítani (pl. a shadowmap blurozásával), mert z-re nem alkalmazható konvolúció (részletes levezetés megtalálható itt). Informálisan gondolkodva: ha megblurozod a shadow mapet, azzal csak annyit érsz el, hogy a mélységértékek egy átlagát hasonlítod az éppen aktuális pontéhoz, ami még mindig 0 vagy 1, de legalább marhaság.

A blur-t tehát az f-re lehet csak alkalmazni, ezt nevezték el percentage closer filtering-nek (PCF). A probléma az vele, hogy költséges (5x5 már jól néz ki de az 25 textúra olvasás), másrészt nem is oldja meg úgy a problémát, ahogy kellene (puhább lesz az árnyék, de attól még lehet pixeles).

A kép egy nagyon extrém esetet ábrázol, de megjegyezném, hogy bármekkora shadowmap felbontással előállhat ugyanez, ha elég nagy jelenetet kell lefednie.

Egy kis trade-off-al jelentős javulás érhető el, amit irregular PCF-nek hívnak, és annyiból áll, hogy nem egy fixen meghatározott szomszédságban végzi el az átlagolást, hanem véletlenszerűen. Ennek az eredménye nagy frekvenciájú zaj lesz, de a szerzők állítása szerint ez sokkal kevésbé vehető észre. Egy korábbi cikkben írtam már erről, úgyhogy nem részletezném (és amúgyis ott a kód). Mézesmadzag gyanánt legyen elég annyi, hogy 25 olvasás helyett 8-al is jobb eredményt ér el...

A PCF és a PCSS egy állandó problémája a shadow acne, amit szintén kitárgyaltam az előbb linkelt cikkben. Röviden a lényege az, hogy a shadowmap véges felbontása miatt a beleírt mélységértékek diszkretizálódnak, így az objektumokon zfightol az árnyék. Négy lehetséges megoldás van erre:

• backface-eket rajzolni a shadowmapbe: ettől light bleeding keletkezhet a PCF-ben
• konstans bias: nehéz jól belőni
• gradient based bias: a felület meredekségével variálja a bias-t
• slope scaled bias: hasonló, de hardveresen; csak akkor működik ha depth-ként megy ki az érték

Mindegyik használható valamilyen szinten, de majd látható lesz, hogy a fejlettebb szűrési módszerek automatikusan kiszűrik a shadow acne-t így nem kell vele nagyon foglalkozni.

Ami még megemlítendő, hogy léteznek ún. shadow sampler-ek, amik hardveresen elvégzik a PCF-et (így kevesebb olvasás is elég). Én ezt sosem használtam, mert kártyafüggő.

Itt most egy kis valószínűségszámítás következik, amiből én mindig is síkhülye voltam, de ennyit azért sikerült felfognom. A végéről közelítem meg a dolgot, mert úgy lehet értelmesen elmagyarázni.

A PCF-nél arra vagyunk kíváncsiak, hogy hány százalékban van árnyékban az adott pixel, azaz mekkora annak a valószínűsége, hogy z < d. Namost erre direkt képlet nincs, a fordítottjára viszont van, amit Chebychev egyenlőtlenségnek hívnak, és az alábbi módon néz ki:

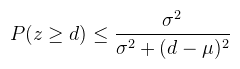Feltételezve, hogy a z, mint valószínűségi változó valamilyen μ várható értékű és σ² szórásnégyzetű eloszlásból való, és d > μ (ez fontos!). A várható értéket jobb helyeken átlagnak is mondják, tehát μ = E(z), ami megfelel a megblurozott shadow mapnek. A másik amire szükség van a szórásnégyzet, amit viszont ki lehet számolni az alábbi képlettel: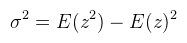


Na és ehhez mi kell? Hát az, hogy a shadowmap ne csak z-t tartalmazza, hanem z²-et is. Tehát a shadowmap GR32F formátumú kell legyen (32 bites float, red és green channel), ami picit több memória. 16 bites float-al is lehet próbálkozni, de az én tapasztalataim szerint nem szép az eredmény. Előbb megmutatnám a kódot, aztán a problémákat:


Ez szép és jó, csak egy baj van vele: nézzük csak meg a Chebychev egyenlőtlenséget: nem egyenlő van ott, hanem kisebb-egyenlő. Tehát amit itt kiszámoltunk az csak egy felső korlát, és nem fog mindig jó eredményt adni. A gyakorlatban ez light bleeding formájában fog megmutatkozni, mégpedig akkor, amikor a mélységértékekben egy nagyobb ugrás van (a szórásnégyzet nagy). Ez egy durva probléma, és következik belőle az is, hogy a shadowmap-be mindent bele kell rajzolni (árnyékvetőket és fogadókat is), sőt értelmes értékkel nem is lehet letörölni (a jelenet teljesen ki kell töltse).


A bleedinget teljesen nem lehet eltüntetni, de csökkenthető az itteni érvelésnek megfelelően: ha egy ilyen "hibás" pixel egyébként teljesen árnyékban lenne, akkor a Chebychev képlet értéke "elég kicsi". Tehát például az alábbi kód elég jól kiszűri a bleedinget:


Ahova ez nem elég, oda alkalmazható a layered VSM technika, ami a shadowmapet diszjunkt régiókra osztja mélység szerint, amikben a szórásnégyzet nem leng ki nagyon. A módszer tehát közel sem használhatatlan, sőt a Crysis használja is a főhős árnyékához.

Most elkezdhetnék itt regélni Fourier sorokról (kiejtés: furié), de úgy az életben nem fogom tudni kiszámolni amit kell. Úgyhogy arról majd a következő matekos cikkben lesz szó. Azért is fölösleges most ismertetni, mert az idevonatkozó cikk se tette ezt meg, hanem a lehető legegyszerűbb utat választotta: H(t)-t felírta egy 2 periodicitású "négyzethullámként" (fordítsd le szebben, hogy square wave), aminek a Fourier sora már ismert.

Azaz H(t) = x_square(t) * 0.5 + 0.5 (érdekes, hogy ez a trükk mennyiszer előjön). Mindenki végiggondolja, hogy ekkor:

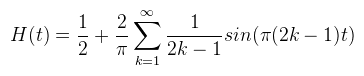Így sokkal egyszerűbben kezelhető a dolog. Mint megbeszéltük, f(d, z) = H(z - d), tehát akkor (és azt a π-t meg beviszem mostmár mert nem férek ki én se):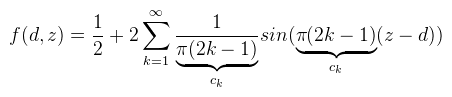


És kihasználva azt az azonosságot, hogy sin(a - b) = sin(a)cos(b) - cos(a)sin(b) kapjuk, hogy: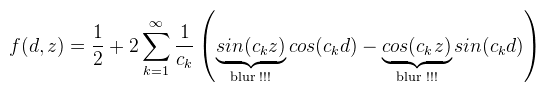


Ha van még olyan elvetemült, aki felírja erre a képletre a konvolúciót is, akkor látható lesz, hogy a blur !!!-al megjelölt részekre előre alkalmazható a konvolúció (tehát elég azt megblurozni). Nem, én nem írtam fel; ha mégsem igaz, akkor az eredeti cikk szerzőinél tessék dörömbölni :) Ugyanide lehet egyébként eljutni a "rendes" Fourier sor definícióból is, csak hússzor ennyi számolással.

Ami zavaró itt az a végtelen szumma, nyilván ez a gyakorlatban nem alkalmazható, de előbb nézzük meg mennyire jó a közelítés ha a szumma csak valami M-ig megy: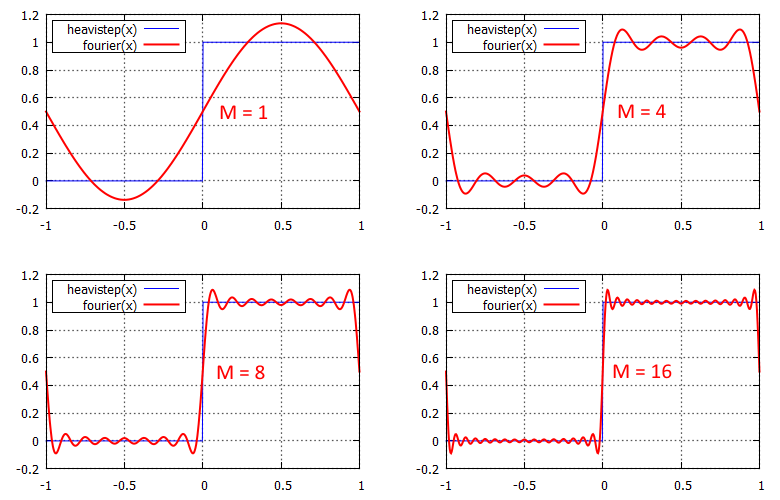


A közelítés láthatóan működik, csak épp van némi probléma vele. Először is hullámos (ezen majd segítünk). A nagyobbik gond, hogy ahogy M növekszik, úgy egyre több sin és cos textúra kell (hiszen minden iterációs lépéshez külön textúrákra van szükség). Mivel a sin és cos olyan, hogy a [-1, 1]-ben veszi fel az értékeit, nyugodtan bepakolhatóak ARGB8 textúrákba, tehát akkor mondhatjuk, hogy egy textúra 4 darab iterációs lépést el tud intézni (azaz M / 2 darab textúra kell összesen).

A spórolás érdekében most csak az M = 4 eset érdekel (de az M = 16 eset adna igazán szép eredmény). Nézzük mit lehet ezzel kezdeni: legyen corrected(x) = (fourier(x + u) - v) * w. Ezzel a képlettel meg lehet úgy buherálni a függvényt, hogy a hullámzásokat egy [0, 1]-be kényszerítéssel eltüntessük: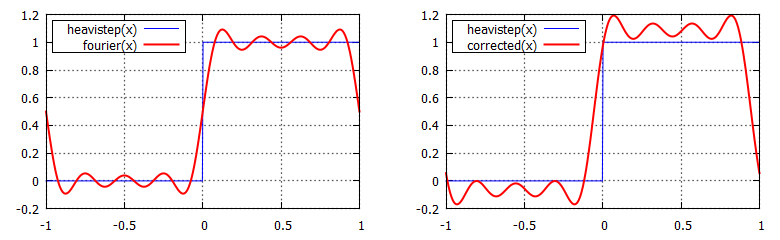


A megfelelő u, v, w értékeket a diagramból is ki lehet következtetni, nekem végül u = 0.055, v = 0.055, w = 1.15 lett a nyerő. Az, hogy 1 környékén mi történik az annyira nem érdekel, mert ekkora távolság ritkán fordul elő egy jelenetben (de jobb értékválasztással az is eltüntethető). Az viszont elég baj, hogy a 0-tól balra a függvény nem elég meredek. Ennek az az eredménye, hogy ha z - d elég kicsi, akkor ott árnyék helyett világosság lesz (tehát még durvábban bleedel, mint a variance shadow).


Speciel egy p hatványra emeléssel lehet rajta segíteni, de ez nem lehet fix érték, mert minél nagyobb annál inkább elrontja az árnyék puhaságát is (hiszen az is ugyanabból adódik, mint a bleeding). Ennek megjavításához meg már kell PCSS (később). Erre a módszerre nem is érdemes több szót pazarolni, ezért kódot sem írok, ugyanis a szerzők is rájöttek, hogy a "korrekció" miatt totál fölösleges Fourier sorokkal küszködni, így született meg az

Merthogy valójában elég lenne azt a nulla környéki részt modellezni, arra pedig az exponenciális függvény teljesen megfelelő. Az új képlet tehát:

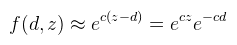Valamilyen c konstanssal. Megint csak z-t sikerült függetleníteni d-től, tehát az azt tartalmazó részre előre alkalmazható a konvolúció (tehát akkor a shadowmapbe e^cz-t kell kiírni). Hasonlítsuk össze a fentebbi Fourier részletösszegből kikatyvasztott függvénnyel: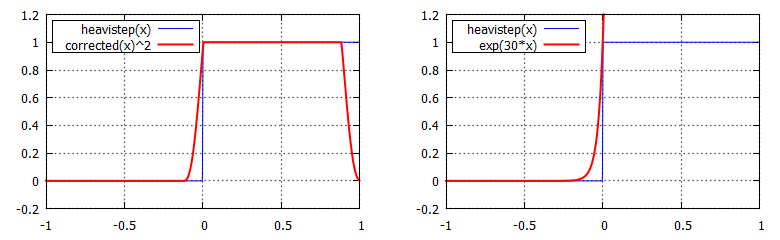


Hát igen, gyakorlatilag halál ugyanaz, sokkal egyszerűbben és olcsóbban. Viszont a baja is ugyanaz: ahogy egyre nagyobb c-t választasz, úgy persze a közelítés is javul, és csökken a light bleeding, de vele együtt az árnyék puhasága is. Ezen is PCSS-el lehet segíteni (dinamikusan variálni c értékét).

Viszont van egy nagyobb probléma, mégpedig az az eset, amikor z > d. A diagramon látszik, hogy a [0, 1] intervallumon a függvénynek (meglepő módon) exponenciálisan nő az értéke, tehát ezekben az esetekben egyrészt a shadow map precíziója drasztikusan romlik (ez a kisebbik a gond), másrészt a blur miatt olyankor is előállhat ez az eset, amikor egyébként nem kéne:


A doboz szélénél (és ezt lehet detektálni a shaderben) a blur miatt a függvény hibás módon átesik ebbe a z > d esetbe, így ott nem tudja elsimítani az árnyékot. Az említett cikk ilyenkor egy PCF-szerű megoldásra fallbackel: egy 2x2-es régióban kiértékeli a függvényt, majd az eredményeket átlagolja. Szerintem baromi ronda. Egyébként sem tetszik nekem ez a két utóbbi módszer (CSM és ESM), mert semmi kedvem hackelgetni a light bleeding eltüntetéséhez.

Ez elsőre elég rejtélyes technikának tűnik, mert senki nem részletezi túl, még az eredeti dolgozat sem. De a lényege egyszerű, mint a kő: (z, z²) és d helyett használjuk ugyanezeknek az exponenciális változatát, tehát (e^cz, e^2cz) és e^cd-t (ahol c egy hasonló konstans, mint előbb). A Chebychev-egyenlőtlenség így egy jobb közelítést tud mondani.

A dolgozat úgy magyarázza ezt, hogy tulajdonképpen nem is a mélysége érdekes az adott shadowmap texelnek, hanem hogy közelebb van-e a fényhez mint egy másik (tehát a relatív eltérés számít). Ha ezt az információt megtartjuk, akkor tetszőlegesen lehet buherálni a shadowmapben szereplő értékeket (ezt hívja a dolgozat monotonic warp-nak).

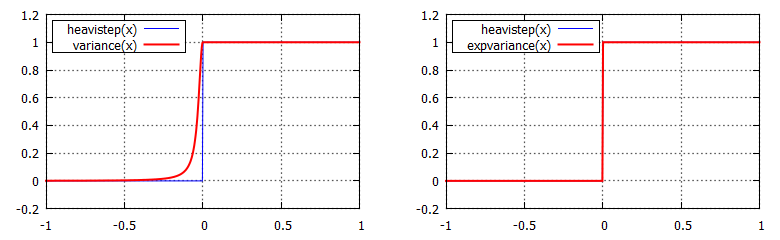Mintha minden álmunk valóra válna...hát sajnos nem, mert a szórástól még mindig függ, bár kevésbé; másrészt az exp használatából adódó hibák megmaradnak (csak a diagram nem tudja kihozni). A dolgozat még ehhez hozzácsap annyit, hogy ne csak ezt a két értéket írjuk ki a shadowmapbe, hanem ennek a negatív változatát is, azaz (-e^-cz, -e^-2cz)-t, majd erre is számoljuk ki a Chebychev-egyenlőtlenség értékét. Ezt az indokolja, hogy nagy c esetén ugyanúgy artifactok keletkezhetnek ha több fogadón is áthalad az árnyék (nem azért, hogy igyon). Én a diagramokon nem tudtam kisilabizálni, hogy mire gondolt, de a lényeg, hogy a végső árnyék a kapott két felső korlát minimuma:


Tehát akkor egy RGBA32F shadowmap kell (plusz ugyanez blurhoz). Hát elég meredek memóriahasználata van, de cserébe az eredmény lényegesen jobb:


A legrondább light bleedinget megszüntette, viszont a doboznál még mindig rossz (holott a dolgozat szerint nem lenne szabad). Szerintem ebben az esetben kéne képbe jönnie a negatív warp-nak; höfö kitalálni, hogy így van-e, és hogyan kell belőni c-t.

Ez nem egy különálló technika, mert bármelyikhez hozzá lehet csapni (bizonyos meggondolásokkal). A lényeg annyi, hogy az árnyék távolabb eső részei puhábbak legyenek, mint a közelebbi részei. A módszer nincs túlmagyarázva sehol, viszont az NVIDIA SDK-ban van rá példakód, úgyhogy én is az alapján dolgoztam.

A módszer azon a feltételezésen alapul, hogy a fény, a blokkoló és a fogadó párhuzamosnak tekinthető (ez persze sokszor nem igaz); ekkor megmondja, hogy mekkora legyen a PCF sugara. Három lépésből áll:

• átlagos mélység meghatározása egy adott régióban (csak blokkolókra)
• penumbra méretének meghatározása
• PCF

Emlékeztetőül a penumbra az árnyéknak az a része, ahol a fényforrás még látszik (amennyiben nem pontszerű). A párhuzamossági feltétel miatt a szükséges értékek meghatározhatóak az alábbi háromszögek hasonlósága alapján:


Ahol a fény sugarát (r) a fény terében kell megadni, tehát r = fény_sugara / frustum_méretei. Az ábrán kiszámolt érték (?) annak a régiónak a sugara, amiben az átlagolást el kell végezni. Megjegyezném, hogy a textúra olvasások száma fix (9x9) és az algoritmus csak az offsetet buherálja, aminek látható következménye van, de legalább hatékony. Legyen ennek a lépésnek a neve findAverageBlockerDepth. Ezek után a penumbra mérete meghatározható az itt leírt képlettel, azaz (inkább kódban írom):


Ábrát ehhez nem rajzoltam, mert a PDF-ben található elég egyértelmű (de az átlagszámoláshoz tartozó nem volt az). Az eredménye elég látványos, de a fix textúra olvasások miatt csíkos. Ez a szemléltetéshez nem baj, a fejlettebb technikákhoz pedig az irodalomjegyzékben található anyag (XXXX Soft Shadow Mapping).


Az első lépés hatékonyságán lehet javítani ún. summed area táblákkal, de ahhoz nem találtam elég anyagot. Maga az algoritmus egyszerű, csak a GPU-n nem trivi kiszámolni (esetleg compute shaderrel).

Mint látható sok módszer van, de én használhatónak csak az (irregular) PCF-et és a variance-ot gondolom, elsősorban a többi módszer memóriaigénye miatt. Ez azért is fontos, mert általában nem elég egy shadowmap a jelenet lefedéséhez, hanem egy "shadow mip chain"-t kell építeni (pl. külső terekhez). Ezekről nem írtam semmit, mert szintén sok van belőlük, de a leghasználhatóbb a cascaded shadow maps és nem is olyan egetrengetően bonyolult.

Egy szűrési módszert kihagytam, amit deferred (soft) shadow-nak hívnak, és a lényege annyi, hogy egy bilateral blur-al postprocess lépésben mossa el az árnyékokat. Ezt könnyen bele lehet integrálni egy létező pipeline-ba, amennyiben shadow mask-ba írod ki a fényekhez tartozó árnyékokat (a Crysis például ezt csinálja). Erről szintén a már említett korábbi cikkben írtam.

Kód a szokott helyen. A diagramokat a gnuplot nevű programmal csináltam.


Höfö:

• Mivel úgyse csinálja meg senki, most nincs höfö.
• Kivéve amiket a cikkben adtam meg!
• Találj ki magadnak höföt (mondjuk rakj rendet a szobádban)!

Irodalomjegyzék

http://www.cad.zju.edu.cn/home/jqfeng/papers/Exponential/... - Exponential Soft Shadow Mapping (EGSR, 2013)
http://research.edm.uhasselt.be/tmertens/papers/... - Real-Time, All-Frequency Shadows in Dynamic Scenes (SIGGRAPH, 2008)
http://developer.download.nvidia.com/presentations/2008/GDC/... - Advanced Soft Shadow Mapping Techniques (NVIDIA, 2008)
http://research.edm.uhasselt.be/tmertens/papers/gi_08_esm.pdf - Exponential Shadow Maps (2008)
http://http.developer.nvidia.com/GPUGems3/gpugems3_ch08.html - Summed-Area Variance Shadow Maps (NVIDIA, 2008)
http://research.edm.uhasselt.be/tmertens/papers/csm.pdf - Convolution Shadow Maps (EGSR, 2007)
http://developer.download.nvidia.com/shaderlibrary/docs/shadow_PCSS.pdf - Percentage-Closer Soft Shadows (NVIDIA)