44. fejezet - A Fresnel egyenletek

Először is hogyan kell kiejteni: frenel. Ugyanis Augustin-Jean Fresnel francia fizikusról van szó, aki leginkább a fény viselkedésével kapcsolatos egyenleteiről ismert. Konkrétan arról szólnak ezek az egyenletek, hogy mi történik a fénnyel akkor amikor egyik közegből áthalad egy másikba (pl. levegőből vízbe). 3D grafika szempontjából két fontos dolog történik vele: egy része visszaverődik, a másik része megtörve továbbhalad (bármilyen viccesen is hangzik).

Emlékeztető általános iskolából

Mondhatnám azt, hogy ott a wikipédia, de akkor nem lenne túl sok értelme cikket írni. Mindenesetre annak könnyebb megértését elősegítendő átrombolnék a fontosabb dolgokon.

Közgazdaságtanból tudjuk, hogy a fény egy elektromágneses hullám, és mint ilyen van neki elektromos mezője és mágneses mezője is. A fény esetében a két mező oszcillációja merőleges a haladási irányra (transzverzális hullám), de bármily meglepő olyan (nem elektromágneses) hullámok is léteznek, ahol az oszcilláció párhuzamos a mozgási iránnyal (longitudinális hullám, pl. hang).

Az elektromágneses hullámok egyik tulajdonsága a polarizáció, ami az oszcillációk viselkedését jellemzi, amennyiben azok egy bizonyos síkban történnek. Például (ha most a haladási irány felől nézzük a hullámot) egy irányban oszcillál csak, vagy esetleg forog. Ha nem egy síkban történik, hanem minden irányban, akkor polarizálatlan (pl. napfény).

Most vegyük az alábbi nagyszerű ábrát, ahol a beeső fénysugár találkozik két közeg határfelületén (pl. levegőben egy üvegfelülettel). Ahogy az előbb említettem a fénynek egy része visszaverődik (reflected ray), a többi része továbbhalad (refracted ray), miközben a felírt egyenlőségek teljesülnek. Az ábrán szereplő n₁ és n₂ a két közeg törésmutatói, levegő esetében 1.000293, üvegben 1.5 körül. Bővebben wikipédia.

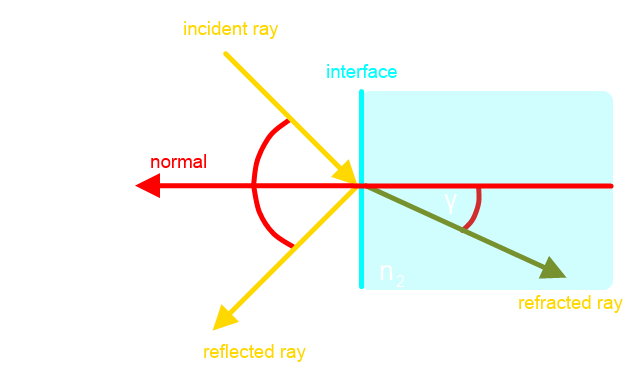
Ezek után A Fresnel-egyenletek két esetet vesznek figyelembe:

a beeső fény eletromos mezője merőleges az ábrára (s-polarizált)
párhuzamos vele (p-polarizált)

és az előbbi wikipédiás linken található egyenlőség teljesül a visszavert fénysugár energiájára (R_s illetve R_p) ezen két esetben:

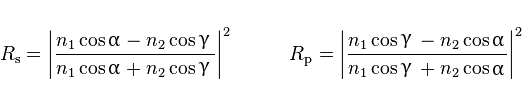
A jó hír az, hogy 3D grafikában csak polarizálatlan fénnyel foglalkozunk, ahol is R = (R_s + R_p) / 2 és a megtört fény energiája pedig T = 1 - R. Ez a két érték (R és T) grafika szempontjából egy szorzót jelent, mint majd látni fogjátok. A még jobb hír, hogy a törésmutató lehet komplex szám is (fémek). Sok sikert kiszámolni, akkor én itt be is fejeztem.

Ez az approximáció sikk

Valójában a fenti képlet már egy az egyben át is írható shaderbe, amennyiben meg tudod határozni a visszavert és megtört vektorokat (szegény vektorok, mindenki csak bántja őket). Kezdjük az egyszerűbb esettel: tükröződés.

Ami annyira nem is egyszerű, mint majd mindjárt kiderül, de első körben csináljuk a klasszikus megoldást, azaz a vizsgálódás középpontjában levő gömb tükrözni fogja a környezetet, amit egy cubemap reprezentál. A logikát némileg meg kell fordítani a shader miatt, tehát a fényforrás úgymond a kamera lesz, de minden ugyanúgy igaz. Tehát a megfordított logika szerinti beeső fénysugár kiszámolható a vertex shaderben, hiszen incray = wpos - eyePos. Az egyenletekhez szükséges másik két vektor meghatározásához pedig vannak beépített HLSL függvények:

CODE

float3 n = normalize(wnorm); // world space normal float3 reflray = reflect(incray, n); float3 refrray = refract(incray, n, n1 / n2);

Javaslom normalizálni őket, hiszen a fenti egyenletekben akkor a koszinuszok egy dot-al elő is állnak:

CODE

float cosA = dot(normalize(reflray), norm); float cosG = -dot(normalize(refrray), norm); float Rs = (n1 * cosA - n2 * cosG) / (n1 * cosA + n2 * cosG); float Rp = (n1 * cosG - n2 * cosA) / (n1 * cosG + n2 * cosA); float R = (Rs * Rs + Rp * Rp) * 0.5f;

Ahonnan a végső szín egy R szerinti lineáris interpolációval áll elő az objektum színe és a cubemapból (a reflektált vektorral) olvasott szín között. Gondolom ezen nincs mit részletezni (ha mégis akkor megnézed a kódot).

Na de...ez a számolás elég soknak tűnik. Van egy olcsóbb módszer, amit Schlick-féle közelítésnek hívnak.

CODE

float3 n = normalize(wnorm); float3 i = normalize(incray); float R0 = (n1 - n2) / (n1 + n2); R0 = R0 * R0; R = saturate(R0 + (1 - R0) * pow(1 + dot(i, n), 5));

R0 itt a Fresnel egyenlet értéke akkor amikor a beeső fénysugár pont a normálvektor irányából találja el a felületet (azaz α = 0). Mindenki végiggondolja, hogy miért így írtam meg a shadert (mert bizony ugyanaz van leírva, mint a wikipédián). Bár az eredeti képletben a félvektor szerepel, a megfordított logika miatt az pont a normálvektor.

Ha valaki azon aggodalmának kívánna hangot adni, miszerint a tükröződés alig látszik, annak javaslom, hogy HDR-ben rendereljen. Milyen jó ötlet, legyen is höfö.

Megfogyva bár, de törve nem

A fénytörés kódján senki nem fog meglepődni.

CODE

float4 reflcol = texCUBE(mytex0, reflray); float4 refrcol = texCUBE(mytex0, refrray); color = lerp(refrcol, reflcol, R);

Mivel ez elég rövidke kód ahhoz, hogy egy egész bekezdést eltöltsek vele, megcsinálom az itt leírt normal mapped effektet is. Mit lehet erről elmondani: aki csinált már normal mappinget az valószínűleg ki tudja találni.

Egy fontos dolog azonban mégis van: zöldfülűek nekiállnának a beeső fénysugarat textúra térbe trafózni (ahogy szoktuk), aztán csodálkoznak, hogy miért nem azt látják amit kéne. Persze, a számolást meg lehet ott is csinálni, de a cubemapből world spaceben kell olvasni. Célszerűbb tehát a normal mapból olvasott vektort átpakolni world spacebe:

CODE

float3 tnorm = tex2D(normalmap, tex).xyz * 2 - 1; float3 t = normalize(wtan); float3 b = normalize(wbin); float3 n = normalize(wnorm); float3x3 tbn = { t, -b, n }; // továbbra se tudom miért így számolja a DX n = mul(tnorm, tbn);

Innentől kezdve pedig ugyanaz a buli, mint eddig. Höfö megcsinálni dupla fénytöréssel.

Breaking bad

Most jön egy elszomorító hír: a fenti fénytörés és tükröződés is hibás. Először is azért mert a fénytörés sosem egyszer történik meg, hanem minimum kétszer (hiszen ki is megy az objektumból). Ezt majd később megmutatom hogyan kell csinálni. A másik problémával viszont már kevesebben vannak tisztában:

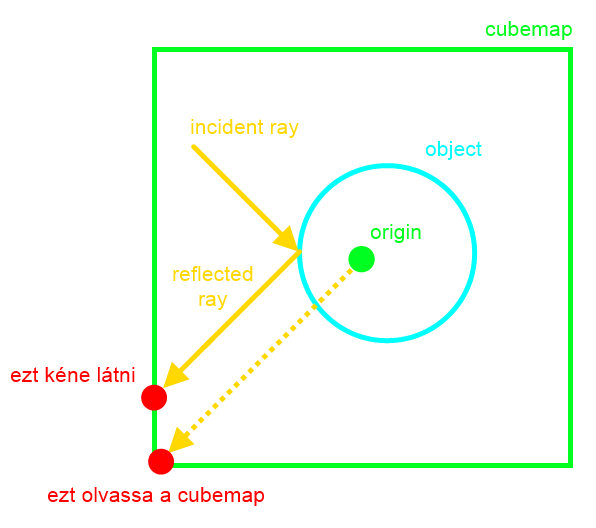
Ugyanis a cubemap címzése mindig az origóból indul. Felmerül a kérdés, hogy hogyan lehet kiszámolni a helyes pontot. Rossz hírem van: csak kereséssel. Ezt nem vázolnám fel, mert egyrészt tüköződés esetén lenyelhető a béka, másrészt fénytöréshez vannak egyéb megoldások is, ahol legalább nem cubemapben kell keresni (később). A linken megtalálható a kód a komplex törésmutatós R0 kiszámolásához is, de én marhára nem látok különbséget.

Friss és nedves

Ha a fénytörés szóba kerül, akkor nem lehet elmenni a víz megjelenítése mellett, ami bár egy bonyolult matematikai modellen alapul, ügyes trükkökkel össze lehet buherálni. A víz animációját továbbra is a normalmap tekerésével oldom meg, a tükröződéshez és töréshez viszont az már említett cikkben leírt módszert fogom alkalmazni.

A víz sík felületnek tekintendő, ezért a cubemap alapű tükröződés nem (annyira) jó rá. Helyette a kamerát (és a fényt is) tükrözöm a víz síkjára és kirajzolom onnan a jelenetet. Csak azt szabad ide belerajzolni, ami tükröződik; ezt legegyszerűbben egy user clip plane-el lehet garantálni. A töréshez használható a (víz előtt) kirajzolt jelenet, de van egy kis gond: abban lehetnek olyan dolgok is, amik a víz fölött vannak, márpedig azok nem kéne látszódjanak a törésben. A cikk javaslata alapján azokat a részeket, amik a víz fölött vannak kimaszkoltam (alpha csatorába belerajzolod 0-val a víz síkját). Ezek után könnyen kiszűrhető az az eset, amikor nem szabad hullámosítani:

CODE

float4 perturbed_refr = tex2D(refractionmap, ptex + distort.xy * 0.02f); float4 masked_refr = tex2D(refractionmap, ptex); float4 final_refr = lerp(perturbed_refr, masked_refr, perturbed_refr.a);

Ahol ptex projektív textúrázással címzi meg a textúrát, ahogy az első shaderes cikkben már említettem. Vigyázat, nem írtam el a lerp-et! Nem az érdekel, hogy az adott pixelben mi van, hanem az ami megtörik a vizen! Ha ott a maszk fehér, akkor az a pixel a víz fölött van, tehát nem szabad használni.

Chromatic dispersion

Magyarul szétszóródásnak hívják, ez szerintem elég pongyola fordítás, hiszen arról van szó amikor egy fénysugár felbomlik a színkomponenseire. Ilyet mindenki látott már aki nem négy fal között él: úgy hívják, hogy szivárvány. Négy fal között élők talán láttak már CD lemezt, az is ezt csinálja.

Ennek az az oka, hogy az anyagok törésmutatója függ attól, hogy milyen hullámhosszú fénnyel találkoznak. Tehát egy mezei fehér fény, amiről azt gondolnád, hogy egyedül utazgat valójában több hullámhosszú (színű) fény kombinációja, amik így különböző szögekben törnek meg.

Rögtön adódik, hogy mit kezdjünk ezzel: mindhárom color channelhez használjunk különböző törésmutatót.

CODE

float n3 = refractiveindices.y + 0.1f; float n4 = refractiveindices.y + 0.25f; float3 refrray1 = refract(i, n, n1 / n2); float3 refrray2 = refract(i, n, n1 / n3); float3 refrray3 = refract(i, n, n1 / n4); // ugyanaz a számolás mint előbb, mindhárom vektorral color.r = lerp(refrcol1.r, reflcol.r, Rr); color.g = lerp(refrcol2.g, reflcol.g, Rg); color.b = lerp(refrcol3.b, reflcol.b, Rb);

Ehhez már SM 3.0 illendő. Persze lehet csalni, például a fresnel érték (R) lehet mindháromra ugyanaz. Egyszeres fénytörésnél nem néz ki egetrengetően, duplával meg nem próbáltam. Höfö megcsinálni szépre.

Rhapszódia

A dupla fénytöréshez nyilván szükség lesz valamilyen formában az objektum belsejére, azon belül is a normálokra, de a feladat megoldásához a pozíciókra is. Az említett cikk az objektum belsejét és a környezetet is cubemapbe rendereli, és abban szekáns kereséssel találja meg a szükséges dolgokat. Először én is ezzel próbálkoztam (jó régen...), de tök fölösleges és rengeteg memória. Szóval jobb ha elfelejted.

Helyette meg lehet azt csinálni, hogy a nézőpontból rendereled ki ami kell, megbékélve azzal, hogy nem mindig lesz pontos. De hát egyébként sem az. Mint majd a demóban is látni lehet a back facek miatt elég idegesítő artifactok jönnek létre. Na de nézzük mit lehet tenni.

Adott az p0 pozíció és a v megtört vektor. A feladat megtalálni a kirenderelt textúrában a belső felület normálvektorát, ami konkrétan a p0 + d * v egyenes és a felület metszetének megkeresését jelenti valamilyen ismeretlen d-re. Szerencsére a megoldáshoz létezik egy kvadratikusan konvergáló algoritmus, amit Newton-Rhapson iterációnak hívnak. Biztos rá lehet húzni a deriváltat erre a szitura is, de egyszerűbben is el lehet magyarázni egy ábrával.

Legyen F(x) = tex2D(positiontex, project(x)).

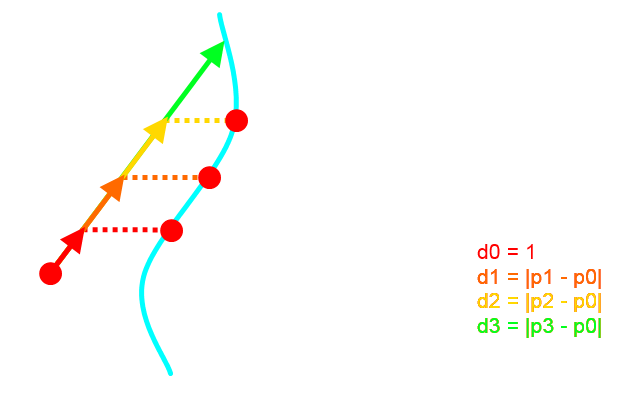
Tehát elindulok egy tetszőleges d-vel (1 eddig jó volt), és lépek a megadott irányban (p0 + d * v). Ezt a pontot levetítve olvasok a pozíciókat tartalmazó textúrából, megkapva p1-et. A következő becslés d-re p1 és p0 távolsága. Ezzel ugyanez történik, mint előbb, megkapva p2-t és így tovább. Az ábrából is látszik, hogy igen gyorsan konvergál, tehát 3-4 iteráció bőven elég.

Annyit hozzátennék, hogy ciklussal implementálva problémák adódtak, nem világos, hogy miért. De ilyen kevés iterációra nem is kell ciklus. Na de akkor hogyan tovább: nevezzük el ezt a függvényt NewtonRhapson2D(outp, outn, p0, v)-nek, ami visszaadja a keresett normált (és a pozíciót is, de az most nem fog kelleni).

CODE

float3 v0 = normalize(x0 - eyePos); // incident ray float3 v1 = refract(v0, n0, ratio); // refracted ray float3 x1, n1; NewtonRhapson2D(x1, n1, x0, v1); v2 = refract(v1, -n1, 1 / ratio); // secondary refracted ray if( dot(v2, v2) > 0 ) refrcolor = texCUBE(mytex0, v2); // hit sky else refrcolor = texCUBE(mytex0, reflect(v1, -n1)); // total internal reflection

Bejött egy új fogalom, amit teljes belső visszaverődésnek hívnak. Ahogy a nevében is benne van, a fény nem tud áthatolni a felületen, mert olyan szögben sikerül eltalálnia. Ez akkor fordulhat elő, amikor n2 < n1. Persze lehetne tovább pattogtatni a sugarat, de minek.

A különbség az egyszeres fénytöréshez képest ordít. Eltekintve persze az artifactoktól és attól, hogy ennél bőven többször meg kéne törjön a fény (pl. teáscsésze füle). De más szempontból is leegyszerűsített eset ez, mivel az objektumon kívül nem raktam be mást a jelenetbe, de a következő bekezdésből kiderül, hogy mit kellene akkor csinálni.

Caustic Armand

Most mindenki utálni fog, de ezt már lusta voltam leimplementálni. Hehe. Amúgy sem egy trivi probléma, mivel a caustic minősége erősen függ a fotonok számától. A rosszabb hír, hogy nem tudsz annyi fotont kipakolni amennyi már jól nézne ki mert diavetítő lesz a programból.

Na de mi is az a kausztika? Pedig minden nap látod ebéd közben: a pohárban levő vízen megtörő fény érdekes mintákat varázsol a terítőre. Zárójelben mondom, hogy visszaverődésből is előállhat caustic.

Kapcsolódik a dupla fénytöréshez is, hiszen ahhoz hogy caustic-ot láss kell valami egyéb objektum is amin az megjelenik (jééé). Ez a gyakorlatban plusz egy geometry buffert jelent, immár a terítő front faceivel. A fénytöréshez is és a caustichoz is kell egy újabb NewtonRhapson2D() hívás, immár ezzel a geometry bufferrel. A fotonokat utóbbihoz nyilván a fényforrásból kell indítani, a végső pozíciókat (a terítőn) pedig el lehet tárolni egy photon buffer-be, ami jobb híján egy textúra. Az alfába pedig a fotonnak a Fresnel egyenletekből kiszámolt energiáját. A második megtörésnél az addig kiszámolt energiát szorozni kell az újjal.

A photon buffer-ből aztán egy rakás algoritmus létezik amivel rekonstruálni lehet a kausztikát, ezek közül a legegyszerűbb az, hogy pont primitíveket rajzolsz ki. Sőt, tulajdonképpen ez a legrészletesebb, viszont zajos (videó). Hát persze, hiszen az ide-oda pattogás miatt egy Monte Carlo-hoz hasonló konvergencia kritérium (de jól leírtam) áll elő, tehát végtelen felbontású photon buffer kéne. Több megoldás létezik:

photon splatting: point spriteokat rajzol ki (mindegyiken egy Gauss eloszlásos minta) additive blendinggel
caustic triangles: a fotonokat összeköti háromszögekbe, az energiát valahogy elmókolja a háromszögeken
adaptív finomítás: tovább finomítja azokat a részeket, ahol ronda (geometry shader kell hozzá)

Az első kettő hatalmas részletességvesztést okoz, a második pedig böszme lassú (viszont szép). Nekem lenne néhány egyéb ötletem (research lehetőségek, akit érdekel és szeretné is csinálni, az keressen meg):

valamilyen brutális új filter: median-t kipróbáltam, nem jó
temporal supersampling: többször kirenderelni a causticot, egy picit más fénypozícióval, az eredményekből rekonstruálni
OpenCL vagy compute shader: az OpenCL integrálása a megoldásba úgy, hogy gyorsabb legyen mint a geometry shaderes
voxel rendering: a foton pozíciókból felépíteni egy skalármezőt, onnan pedig nem háromszöges megoldással renderelni
inverz rekonstrukció: direktbe kirenderelni a caustic mintát, úgy hogy "visszafelé követed" a fotonokat

Illetve ott van persze a path tracing, ami ezeket ingyen adja, de a hardver még nem bírja el normális sebességgel, tetszőleges geometriára. Megemlítenék viszont még egy érdekes research témát: 3D caustic, azaz egy 4D objektum által generált caustic minta. Igen látványosnak képzelem.

Summarum

Érdekes módon ha valaki azzal akarja reklámozni a cuccát, hogy az milyen valósághű, akkor valamilyen tükröződő effektet rak bele. Persze az nem az engine érdeme, hanem a tükrözött környezeté, ami tipikusan egy fényképezővel készített HDR kép. Úgy meg naná, hogy valósághű...el is nevezték image based lighting-nak, erről már volt szó a HDR cikkben. Mindenesetre az itt leírt dolgok felhasználhatóak nem csak IBL-ben, hiszen egy specular lightingra ugyanezek az egyenletek alkalmazhatóak.

Balról jobbra: *dispersion (felül), egyszeres refract, kétszeres refract*

Megjegyzés: a chromatic dispersion nem keverendő össze a chromatic abberation-al, ami bár ugyanazon ok miatt jön létre de egy zavaró effekt. Sok irodalom mégis ezt az elnevezést használja.

Kód github-on (jobb oldalt van "download zip" gomb).

Höfö:

Csináld meg HDR-el!
Csináld meg a dispersion-t dupla fénytöréssel!
Találj nekem egy jó stained glass (templomokban) textúrát és normal mapet!

Irodalomjegyzék

http://en.wikipedia.org/wiki/Fresnel_equations - Fresnel egyenletek (wikipédia)
http://en.wikipedia.org/wiki/List_of_refractive_indices - Néhány anyag törésmutatója (wikipédia)
http://http.developer.nvidia.com/GPUGems2/gpugems2_chapter19.html - Egyszeres fénytörés (GPU Gems)
http://http.developer.nvidia.com/GPUGems3/gpugems3_ch17.html - Többszörös fénytörés (GPU Gems)
http://sirkan.iit.bme.hu/~szirmay/gpucaust5.pdf - Caustic (BME)