Ez megint egy olyan cikk, amihez nem lesz kód, ezért igyekszem matematikailag levezetni amit csak lehet. A feladat az, hogy egy 3D objektumot (ami jelen esetben egy vágósík) az egérrel (illetve tableten ujjal) lehessen húzogatni de úgy, hogy a mozgás pontosan kövesse az egeret.

A megoldás két darab metódus implementálására szorítkozik. Az onmousedown() egyszer hívódik meg, ekkor az állapot beáll arra, hogy most cibálod az objektumot. Meghatározandó egy 3D pont, amit éppen tapicskolsz. Az onmousemove()-ban hasonló a feladat, és kiszámolandó az objektum új pozíciója. Ha felengedted az egeret, akkor az állapot visszaáll üresre.

Kiemelném, hogy bár én itt egy síklapot ráncigálok, tetszőleges objektumra ugyanígy lehet eljárni, amennyiben meg tudod határozni egy sugárral való metszetét.

Az első lépés könnyű, hiszen csak meg kell határozni egy sugarat az aktuális kamerából, és kideríteni a metszetét az objektummal.

Megjegyzem, hogy vektorokat nem lehet vetíteni, tehát két levetített pontból kell meghatározni. Az Unproject() függvényt nem kell nagyon magyarázni, mert csak átkonvertálja a pontot a [-1, 1] x [1, -1] tartományba, beszorozza a mátrixxal és leoszt w-vel.

Jelen esetben az objektum egy síkdarab (mint egy papírlap), amihez könnyű meghatározni a metszetet a síkegyenletből, illetve a sík tangent frame-jéből. Ugyanis, vegyük az (a, b, c, d) síkot, és az (s, r) sugarat, ekkor:

n := (a, b, c) <n, s + tr> + d = 0 <n, s> + t<n, r> + d = 0 t = -(d + <n, s>) / <n, r>

Ez azt jelenti, hogy a sugár egy pontja rajta van a síkon, aminek persze előfeltétele, hogy a sugár nem párhuzamos a síkkal, ezt höfö lekezelni.

A másik meggondolás az, hogy ha a síklapnak ismered a koordinátáit, akkor abból meg lehet kapni egy u = v1 - v0 és v = v3 - v0 vektort. Márpedig az, hogy egy x pont rajta van a síklapon azt jelenti, hogy felírható ilyen alakban:

x = v0 + λu + μv     (λ, μ ∈ [0, 1])

Ebből mátrix egyenletet csinálva:

b := (λ, μ, 0, 1)T M :=  [ ux vx nx v0x ]  [ uy vy ny v0y ]  [ uz vz nz v0z ]  [ 0 0 0 1 ] Mb = x    ->    b = M-1x

És csak le kell ellenőrizni, hogy a kapott értékek a [0, 1] intervallumban vannak-e.


Na de a probléma: mozgatáskor ebből a kapott pontból, illetve egy másik (egyébként ismeretlen) pontból kéne meghatározni, hogy a sík hol lesz. Hogy ne legyen olyan könnyű a dolog, a síkot csak a normálvektora mentén lehet mozgatni, azaz az egér pozíciójának köze nincs a most kiszámolt ponthoz!

Ez egy hihetetlenül triviális megoldás: azt feltételezzük, hogy a keresett másik 3D pont ugyanazzal a t1 paraméterrel jön ki, mint előbb. Ez azért merül fel egyáltalán, mert annyit azért tudunk, hogy az új pontot a mozgatás vektora mentén kell keresni.

Mi is történik itt? Azt mondom, hogy az új pont ugyanolyan messze van a közeli vágósíktól, mint az előbb kiszámolt. Mivel a mozgatás meg van szorítva a sík normálvektorára, az új pontot még rá kellene vetíteni, de vegyük észre, hogy a levetített pont is ugyanolyan messze lenne a síktól, így ezt meg lehet spórolni.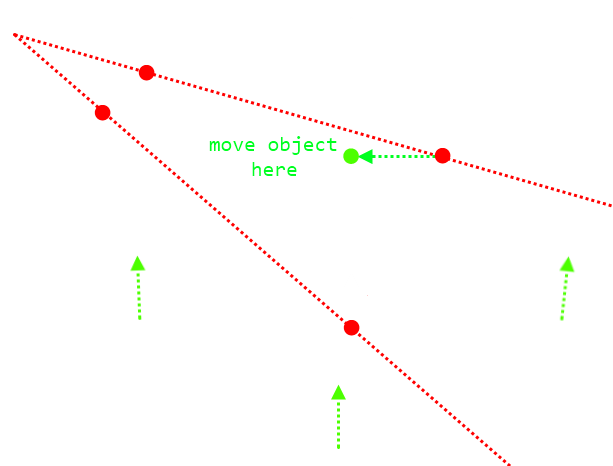


A feltételezés gyakorlatilag soha nem igaz (kivéve párhuzamos vetítéssel), viszont olcsó és többnyire használható. Azaz ha a mozgás iránya nem merőleges az XZ síkra, akkor nem követi rendesen az ujjad (és ez is csak addig igaz amíg "normális" kamerád van).

Ahogy elnéztem az 3ds Max-ot, az is valami hasonló dolgot csinál. Mivel az egér tetszőlegesen elkalandozhat a mozgatásra kijelölt egyenestől, érdemesebb meghatározni egy síkot, ami tartalmazza az egyenest. A probléma csak az, hogy ez a bizonyos sík nagyon nem egyértelmű.

A gondolatmenet a következő: az aktuális mozgásirányra merőleges síkok közül válasszuk ki a legjobbat. A legjobb legyen az, ami leginkább a kamera felé néz. Vegyük, most az (a, b, c, d) síkot, ekkor az alábbi három lehetőség jön szóba:

p1 = (-b, a, c, d) p2 = (-c, b, a, d) p3 = (a, -c, b, d)

Valójában van még három lehetőség, de azok a probléma szempontjából ugyanezek (másik irányba néz). Ebből a háromból viszont csak kettő merőleges az eredeti síkra.


A használat elég nyilvánvaló: a mozgatáshoz szükséges második pont a sugár és a kiválasztott segéd sík metszete lesz, szintén rávetítve még az eredeti sík normáljára.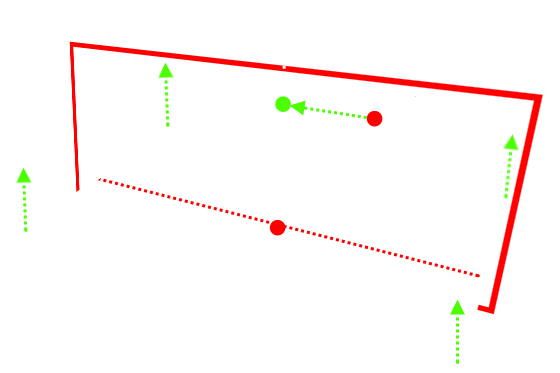


Viszont van olyan eset, amikor mindegyik sík rossz, például ha a kamera az ábrán szereplő síkot majdnem felülről nézi. Ekkor mindkét segéd sík nagyon éles szögben látszik és nehézkes a mozgatás, sőt nem is mindig egyértelmű hogy merre kell mozgatni az egeret.

Ez alatt azt kell érteni, hogy amennyire csak tud, a kamera felé fordul (a mozgásirány tengelye körül foroghat). Ez azért jó, mert nem kell válogatni a síkok között: a kamera nézési irányát rávetítem az aktuális síkra, és az lesz a segéd sík normálvektora.

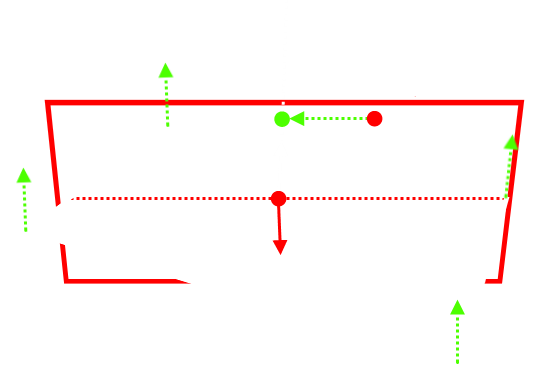
Ez az előbbi problémát nem oldja meg, és bizonyos esetekben a segéd sík elég idióta és természetellenes irányokba kell mozgatni az egeret, hogy az történjen amit akarsz (pl. ha az objektumot az X tengely mentén akarod ráncigálni).

Ez a lusta programozók módszere: felejtsük el a problémát. A baj ugye az, hogy az egér elkalandozott a mozgatás egyenesétől. Semmi gond, vetítsük le rá screen space-ben, ezzel a feladat máris sokkal egyszerűbb, hiszen az ebből kapott sugárra:

trackpos + λn = s + μr

Hát és akkor mivan, van két ismeretlened, ezzel mihez kezdesz? Felhívnám a figyelmet arra, hogy a fenti egyenlet valójában három darab egyenlet (x, y és z koordinátára). Tehát az egyenletrendszer túlhatározott, ami azért valamivel jobb. Vadul fel is írom mátrix alakban:

b := trackpos - s x := (μ, -λ, 0, 1) M :=  [ rx nx 0 0 ]  [ ry ny 0 0 ]  [ rz nz 1 0 ]  [ 0 0 0 1 ] Mx = b

És itt most álljunk meg egy pillanatra, ez ugyanis nem egy szokványos mátrix. Tudjuk, hogy inverz akkor létezik, ha a determináns nem nulla. Ennek a mátrixnak a determinánsa könnyen kiszámolható a harmadik oszlop szerint kifejtve:

det(M) = nxry - rxny

Ami bizony vidáman lehet nulla igen sok esetben. De mi tűnik fel? A harmadik sornak köze nincs a determinánshoz, ez meg miféle dolog? Azért kéremszépen, mert ennek az egyenletrendszernek nem ez az egyetlen mátrix alakja. Fel is írom a másik kettőt:

M :=  [ rx nx 1 0 ]  [ ry ny 0 0 ]  [ rz nz 0 0 ]  [ 0 0 0 1 ]

M :=  [ rx nx 0 0 ]  [ ry ny 1 0 ]  [ rz nz 0 0 ]  [ 0 0 0 1 ]

Így mindjárt jobb a helyzet: van három esély arra, hogy a determináns ne legyen nulla. Ha mindhárom esetben nulla, akkor nincs megoldás, ez akkor fordul elő, amikor pontosan merőlegesen nézel a tapizott síkra.


A megoldás tök jó, a működés viszont érdekes. Tipikusan akkor mozog jól az objektum, ha a screen space-beli normálvektor mentén mozgatod. A baj az, hogy ezt egy átlag user marhára nem fogja fel.

Na de akkor melyik megoldás a legjobb? Őszinte leszek: halvány fingom sincs. Mint mondtam, a 3ds Max az 1. megoldást használja, a BIMx a 0. megoldást (mivel ott csak fel/le lehet mozgatni), én az engine-ben a 3. megoldást hagytam meg, kiegészítve egy nagyon aranyos ugráló kék nyíllal, ami mutatja a usernek, hogy merre kell húzni az ujját.

Kéne még alá valami bumszli...


Höfö:

• Implementáld le a 4., 5. és 6. megoldást!
• Küldd el nekem...