Rendíthetetlenül tovább haladva a physically based rendering már kitaposott, helyenként mocsaras, néhol kövekkel teleszórt ösvényén (melyen rendkívül egyszerű elzanyálni), elérkezünk a szakmai berkekben state of the art-nak nevezett megjelenítési módszerekhez, melyek közül a path tracing, illetve a hozzá kapcsolódó fejlettebb technikák kombájnként tarolják le az előttük felmerülő problémák gyanútlan mezejét (és persze a programozó haját is).

Path tracing-ről minimálisan volt már szó, például a GTAO kapcsán, viszont többnyire az intuitív oldalról közelíttetem meg, mellőzve a teljesértékű formális le- és felvezetést. Az elmúlt években azonban felkapott téma lett a hardveres ray tracing, ami miatt a veteránnak számító grafika programozók is kellve-kelletlenül rákényszerülnek a téma legalább felületes megismerésére. Ezen felületes megismerésről szól ez a cikk. Sejthető, hogy a korábbiakhoz képest sem triviális dolgokról lesz szó.

A történet szokás szerint matematikai háttérrel kezdődik, viszont utólag jöttem rá, hogy nem lehet értelmesen megszabdalni (merthogy minden függ mindentől). Ellenben most is igaz, hogy aki tisztában van a megfelelő fogalmakkal (avagy nem érdekli), az átugorhatja az első néhány bekezdést és kezdheti rögtön a Monte Carlo integrálással.

A további részek úgy vannak strukturálva, hogy akik csak mellékszálon szeretnének foglalkozni a témával, azoknak elegendő információ legyen a path tracing lényegéről (de itt is átugorhatóak dolgok), haladó fejlesztőknek pedig mutatok egy teljesértékű, tisztán compute shader alapú megoldást.

Irodalomként Eric Veach nevezetes doktori dolgozatát és a PBR bibliát (a továbbiakban 'könyv') használtam, az eredmények validálásához pedig a Mitsuba nevű programot.

BREAKING: A fontosabb képek mostantól modal dialog-ban jelennek meg (X-re tappolva, vagy Esc-et nyomva lehet bezárni).

Mivel sok új fogalom lesz bevezetve, a használt matematikai szimbólumok jelentését ismét kigyűjtöttem. Feltételezem viszont, hogy az olvasó tisztában van a Cantor-féle halmazelmélettel és az alapvető differenciál- és integrálszámítási fogalmakkal.

Jelölés	Magyarázat
∅	üres halmaz
ℝ	a valós számok halmaza
ℝn	ℝ önmagával vett n-szeres Descartes-szorzata
ℝ	ℝ ∪ { -∞, ∞ }, a valós számok bővített halmaza
ℝn	ℝ önmagával vett n-szeres Descartes-szorzata
ℬ(ℝn)	ℝn Borel-mérhető halmazai
𝒫(X)	az X halmaz hatványhalmaza
σ	görög (kis) szigma betű
Σ	görög (nagy) szigma betű (σ-algebra jelölése vagy szummázás)
μ	görög mű betű (mérték jelöléséhez)
ν	görög nű betű (mérték jelöléséhez)
ν ≪ μ	a ν mérték abszolút folytonos a μ mértékre nézve
λ	görög lambda betű (Lebesgue-mérték vagy radiometriában hullámhossz)
ℒ	a Lebesgue σ-algebra
ω	görög (kis) omega betű (irányokhoz)
Ω	görög (nagy) omega betű (valszámban a kimenetelek halmaza, egyébként tartomány)
ξ	görög xí betű (valségi változó jelöléséhez)
ζ	görög zéta betű (valségi változó jelöléséhez)
φ	görög fí betű (azimut szög)
θ	görög théta betű (magassági szög)
E[ξ]	a ξ valségi változó várható értéke
Var[ξ]	a ξ valségi változó szórásnégyzete (varianciája)
β	valszámban a közelítő torzítása, egyébként path throughput weight
ρ	görög ró betű (albedo szín)
η	görög éta betű (törésmutató jelöléséhez)
∏	görög (nagy) pí betű (produktum)
inf	infimum; (halmaz) legnagyobb alsó korlát(ja)
sup	supremum; (halmaz) legkisebb felső korlát(ja)
∀	univerzális kvantor; ejtsd: "minden" vagy "bármely"
∃	egzisztenciális kvantor; ejtsd: "létezik"
⇒	implikáció; ejtsd: "[-ból] következik [, hogy]"

Amikor olyanokat mondok, hogy "jelöljük", "nevezzük", stb., akkor az alatt a magyar/orosz notációt értem, amitől pl. az angol/német eltér. A jelölések lehetnek kontextusfüggőek, ilyenkor máshogy vannak formázva (dőlt, félkövér, stb.). Kötőszó gyanánt helyenként a latin id est ("azaz") és exempli gratia ("például") kifejezéseket használom, hogy ne unatkozzak.

Eddig, amikor integrálásról volt szó, akkor vagy mellőztem a konkrét definíciót, vagy visszavezettem Riemann-integrálra. Amit erről tudni kell, hogy csak véges és zárt intervallumokon van értelmezve (ill. az integrálandó függvény ezen intervallumon korlátos kell legyen). Az egyik kiterjesztése az ún. improprius Riemann integrál, ami az előbbitől eltérő esetekben az integrál határértékét veszi. Egy másik problémája, hogy függvénysorozatok esetében a határérték csak bizonyos feltételek mellett hozható ki az integráljel alól (az ún. monoton konvergencia tétel nem teljesül).

A későbbi bekezdésekben ismertetett matematikai fogalmak egy modernebb kiterjesztést, az ún. Lebesgue-integrált (kiejtés: löbeg) használják, ami magasabb dimenziókban is lényegesen kevesebb korlátozással használható. A technikai részleteket és tételbizonyításokat elhagyva ezt vezetem fel először.

Definíció (hatványhalmaz): az X halmaz hatványhalmazának nevezzük, és 𝒫(X)-el jelöljük az X összes részhalmazainak halmazát (beleértve az üreshalmazt és X-et is).

Például, ha X = { 1, 2, 3 }, akkor 𝒫(X) = { ∅, { 1 }, { 2 }, { 3 }, { 1, 2 }, { 1, 3 }, { 2, 3 }, { 1, 2, 3 } }

Definíció (σ-algebra): legyen 𝒫(X) valamilyen X halmaz hatványhalmaza, ekkor a Σ ⊂ 𝒫(X) halmazrendszert az X feletti σ-algebrának nevezzük, ha:

• X ∈ Σ (tartalmazza a kiinduló halmazt)
• ha A ∈ Σ, akkor X\A ∈ Σ (zárt a komplementerképzés műveletére)
• ha A₁, A₂, A₃, ... ∈ Σ, akkor A₁ ∪ A₂ ∪ A₃ ∪ ... ∈ Σ (zárt a megszámlálható únióképzés műveletére)

Az (X, Σ) rendezett párt mérhető térnek, Σ elemeit pedig mérhető halmazoknak nevezzük. A definíció alapján könnyen belátható, hogy egy σ-algebra az (véges vagy megszámlálhatóan végtelen sok) elemeinek únióit és metszeteit is tartalmazza.

Az ℝⁿ nyílt halmazai (i.e. nem tartalmazzák a határmenti pontokat) által generált σ-algebra (jelölésben ℬ(ℝⁿ)) elemeit az ℝⁿ Borel-mérhető halmazainak hívjuk.

Definíció (mérték): legyen Σ az X halmaz feletti σ-algebra, ekkor a μ : Σ → [0, ∞] függvényt mértéknek nevezzük, ha

• μ(∅) = 0
• ∀ E₁, E₂, E₃, ... ∈ Σ páronként diszjunkt, megszámlálható halmazsorozatra:
  
  (σ-additivitás)
  

A mérték fogalmát a valós számtengelyen értelmezett "hossz" absztrakciójaként fejlesztették ki. Az itt bemutatott definíció ennél általánosabban, halmazokra fogalmazza meg. Konyhanyelven az mondható, hogy a mérték a "méret" fogalomnak egy absztrakt változata.

Klasszikus példa a számláló mérték, ami az A ∈ Σ halmazokhoz hozzárendeli az elemszámukat.

Az (X, Σ, μ) hármast mértéktérnek nevezzük. Ha minden nullmértékű halmaz összes részhalmaza mérhető, akkor mértéktér illetve a mérték teljes.

Amennyiben μ(X) = 1, akkor a mértékteret valószínűségi mezőnek, Σ elemeit eseményeknek, μ-t pedig valószínűségnek hívjuk (ez később is meg lesz említve).

Definíció (külső mérték): legyen 𝒫(X) valamilyen X halmaz hatványhalmaza, ekkor a μ^* : 𝒫(X) → [0, ∞] függvényt külső mértéknek nevezzük, ha

• μ^*(∅) = 0
• tetszőleges A, B₁, B₂, B₃, ... ∈ 𝒫(X) halmazokra,
  
  (szubadditivitás)
  

Az elnevezés onnan jön, hogy az A halmaz mértékét "kívülről" közelíti a B_j halmazok mértékeivel ("túllógva" fedik le A-t). Erre a köztes fogalomra azért van szükség, mert egyelőre nem tudunk mértéket konstruálni. Az alábbiakból viszont kiderül, hogy ha külső mértékre ezt meg tudnánk tenni, akkor abból egy egyszerű feltétel hozzáadásával már mértéket kapunk.

Definíció (μ^*-mérhetőség): legyen μ^* külső mérték az X halmazon, ekkor az E ⊂ X halmaz μ^*-mérhető, ha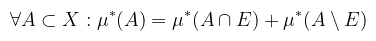


Értsük ezt úgy, hogy ha veszek bármilyen A halmazt, és két részre vágom az E halmazzal ("kimaszkolom"), akkor az nem változtatja meg az A halmaz külső mértékét (ld. Carathéodory-kritérium), i.e. megegyezik a két rész külső mértékének összegével.

Tétel (külső mérték konstruálása): legyen ℋ ⊂ 𝒫(X) halmazrendszer, ν : ℋ → [0, ∞] függvény, ν(∅) = 0, E ⊂ X és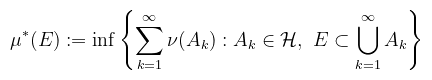


ekkor μ^* külső mérték és a ν-höz tartozó külső mértéknek nevezzük.

Ez azt jelenti, hogy legenerálom az összes lehetséges "túllógó" lefedést és veszem ezeknek a legnagyobb alsó korlátját. Intuitívan tehát valóban külső mértéket készítettem.

Vegyük észre, hogy a lefedést alkotó halmazokra nincs kikötve sem az, hogy véges sokan vannak, sem az, hogy mérhetőek. Továbbá, E-re nincs kikötve, hogy korlátos (és így körvonalazódik, hogy a majd ebből képzett integrálfogalom általánosabb lesz a Riemann-integrálnál).

Tétel (mérték konstruálása): legyen μ^* külső mérték az X halmazon, Σ az X μ^*-mérhető részhalmazainak halmazrendszere és μ a μ^*-nak a Σ-ra vett megszorítása. Ekkor (X, Σ, μ) teljes mértéktér.

Ha X a valós számok halmaza (ℝ) és ν-t a zárt, nyílt vagy félig nyílt intervallumok hosszaként definiáljuk, akkor az ehhez tartozó külső mérték a Lebesgue külső mérték (λ^*), a λ^*-mérhető intervallumok halmaza a Lebesgue σ-algebra (ℒ), melynek elemei a Lebesgue-mérhető halmazok, és λ^*-nak az ℒ-re vett megszorítása a Lebesgue-mérték (λ).

Az ℝⁿ-re való megfogalmazás teljesen hasonló, az intervallum szót téglára (intervallumok Descartes-szorzata), a hosszt pedig a megfelelő analóg fogalomra cserélve (intervallumok hosszainak szorzata). A jelölések ilyenkor ℒⁿ illetve λⁿ (n-dimenziós Lebesgue-mérték).

Konyhanyelven λ-t hossznak, λ²-et területnek, λ³-at térfogatnak nevezzük. Térfogatból lehet levest is főzni, ami nem finom, de azért sok.

Definíció (μ-majdnem mindenütt): legyen (X, Σ, μ) mértéktér és ℓ : X → { igaz, hamis } logikai függvény. Legyen H ⊂ X az a halmaz, ahol ℓ értelmezett és az értéke igaz. Azt mondjuk, hogy ℓ μ-majdnem mindenütt teljesül X-en, ha X/H nullmértékű.

Tehát valamilyen tulajdonságra akkor mondjuk, hogy μ-majdnem mindenütt (röviden μ-m. m.) teljesül, ha egy nullmértékű halmaz kivételével mindenhol teljesül.

(megj.: az ilyen szavakat, hogy "mindenhol", részhalmazokra is lehet érteni; a fenti egy egyszerűsített definíció)

Definíció (mérhető függvény): legyenek (X, Σ) és (Y, T) mérhető terek. Egy f : X → Y függvényt mérhetőnek nevezünk, ha minden E ∈ T halmaz f-szerinti ősképe eleme Σ-nak. Formálisan: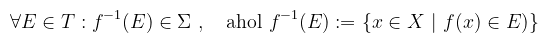


Ha (Y, T) = (ℝⁿ, ℬ(ℝⁿ)) és μ egy Σ-n értelmezett mérték, akkor a függvényt μ-mérhetőnek nevezzük (i.e. minden Borel-mérhető halmaz ősképe mérhető).

Speciel ha (X, Σ) = (ℝ, ℒ) és (Y, T) = (ℝ, ℬ(ℝ)), illetve μ = λ, akkor az f : ℝ → ℝ függvény Lebesgue-mérhető.

Ami még megemlítendő, hogy a valószínűségi változók mérhető függvények a valószínűségi mezőkön.

Definíció (integrál): maga a fogalom továbbra is hasonlót jelent, mint eddig: valamilyen függvény alatti "terület", tehát egy valós szám (vagy végtelen). A függvény viszont most tetszőleges halmazon van értelmezve, amire nem tudunk úgy felosztást készíteni, mint a Riemann-integrál esetében. A felosztást ezért az értékkékészletre csináljuk meg és a függvény segítségével állítjuk elő a közelítést.

Legyen (X, Σ, μ) mértéktér, f : X → [0, ∞] μ-mérhető, és definiáljuk az alábbi halmazrendszert: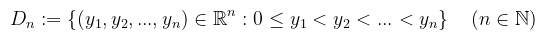


ami tehát a nemnegatív valós számok összes lehetséges n-elemű felosztásainak halmazrendszere.

Egy y = (y₁, y₂, ..., y_n) ∈ D_n-re legyenek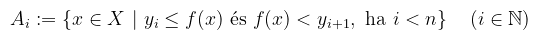


Ez a definíció rendkívül könnyen félreértelmezhető, úgyhogy kicsit részleteném, hogy mit jelent. Adott egy y felosztás a függvény értékkészletén, amihez felosztást keresek az értelmezési tartományban: ezt a felosztást alkotják az A_i halmazok.

A félreértés abból adódik, hogy például az angol wikipédia ezt úgy mutatja be, mintha "vízszintes gerendákkal" próbálnám közelíteni a függvény alatti területet (egyébként lehet), de ez ebben a felírásban nem igaz!

Az A_i halmazok tehát X-nek egy y-hoz tartozó felosztását adják meg, és a függvény alatti "függőleges oszlopok alapjai". Egy adott ilyen A_i "alapnak" a mérete μ(A_i).

Ekkor az f függvény y-hoz tartozó integrálközelítő összege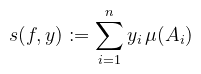


i.e. az "oszlopok" méreteinek összege.

Az f függvény integrálja pedig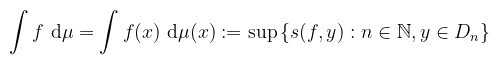


Vagyis az összes lehetséges felosztásból képzett integrálközelítő összeg legkisebb felső korlátja.

Még nem vagyunk készen, hiszen a definíció elején feltettük, hogy a függvény nemnegatív. Tetszőleges f : X → ℝ μ-mérhető függvény integrálját úgy képezzük, hogy kettéválasztjuk a pozitív és negatív részére: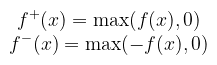


Arra kell ügyelni, hogy a két rész integrálja közül legalább az egyik véges legyen, ekkor azt mondjuk, hogy az f-nek létezik integrálja, és azt a két rész integráljának különbségeként kapjuk meg.

Definíció (mérhető halmazon vett integrál): legyen (X, Σ, μ) mértéktér, f : X → ℝ és E ∈ Σ. Azt mondjuk, hogy az f-nek létezik integrálja az E halmazon, ha a megadott f*-nak létezik integrálja, ekkor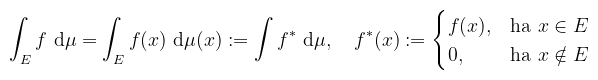


Ha ennek az értéke valós (véges), akkor f-et integrálhatónak nevezzük E felett.

Különbség van tehát aközött, hogy egy függvénynek létezik-e integrálja és hogy integrálható-e. Utóbbinál feltétel, hogy az integrál véges legyen.

Amennyiben μ az n-dimenziós Lebesgue-mérték (λⁿ), akkor az integrált Lebesgue-integrálnak nevezzük (de a továbbiakhoz n = 1-et feltételezek).

Néhány megjegyzés, biz. nélkül:

• nullmértékű halmazon vett integrál nulla
• diszjunkt mérhető halmazok úniójára nézve az integrál additív
• minden Riemann-integrálható függvény Lebesgue-integrálható és az integrálok értéke megegyezik

Ezzel kapcsolatban nyilván a fordított eset az érdekesebb:

Tétel (Lebesgue-kritérium): az f : [a, b] → ℝ (a, b ∈ ℝ, a < b) korlátos függvény pontosan akkor Riemann-integrálható, ha λ-majdnem mindenütt folytonos [a, b]-n.

Ilyenkor persze alkalmazhatóak a Riemann-integrálnál tanult tételek (pl. Newton-Leibniz). Ne felejtsük el azonban, hogy Lebesgue-értelemben nem definiáltunk olyan fogalmat, hogy primitívfüggvény (i.e. határozatlan integrál)! Amennyiben mégis használom, akkor implicit feltételezem, hogy a Lebesgue-kritérium teljesül.

Mielőtt rátérnék a valszámra, ebben a rövid bekezdésben ismertetek egy fontos tételt, ami a különféle mértékek közötti átváltást teszi lehetővé. Kiemelt szerepe van a (valószínűségi) sűrűségek közötti konverziónál.

Definíció (σ-végesség): legyen (X, Σ, μ) mértéktér. Az A ⊂ X halmazt σ-végesnek mondjuk, ha létezik A_i ∈ Σ halmazrendszer úgy, hogy

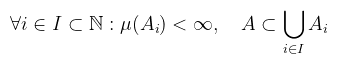
Tehát az A halmaz lefedhető véges mértékű A_i halmazok úniójával. Ha maga az X halmaz σ-véges, akkor a mértékteret és a mértéket is σ-végesnek nevezzük.

Definíció (mérték abszolút folytonossága): legyen ν és μ két mérték ugyanazon az (X, Σ) mérhető téren, ekkor ν abszolút folytonos μ-re nézve (ν ≪ μ), ha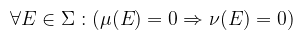


Az implikáció tulajdonságai miatt a jelölés nem részbenrendezést (≤) jelent: a reflexivitás és a tranzitivitás teljesül, az antiszimmetria viszont nem (de a szimmetria sem). Emiatt két mértéket akkor tekintünk ekvivalensnek, ha kölcsönösen abszolút folytonosak (i.e. ν ≪ μ és μ ≪ ν).

Úgy is meg lehet fogalmazni, hogy ν abszolút folytonos μ-re nézve, ha minden μ-nullmértékű halmaz ν-nullmértékű is (de fordítva nem feltétlenül!).

Tétel (Radon-Nikodym): legyen ν és μ két σ-véges mérték az (X, Σ) mérhető téren. Ha ν ≪ μ, akkor létezik f : X → [0, ∞) μ-mérhető függvény, amelyre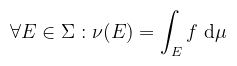


Ekkor a dν/dμ := f függvényt a ν-nek μ-re vonatkozó Radon-Nikodym-deriváltjának nevezzük, és ez a függvény μ-majdnem mindenütt egyértelmű (tehát ha van egy hasonló g függvény is, akkor f = g μ-m. m.).

Ez elsősorban a valószínűségszámításban játszik szerepet (f ún. sűrűségfüggvény), de amint látni fogjuk, tulajdonképpen végig Radon-Nikodym-deriváltakkal dolgozunk majd, csak fölösleges mindenhol felemlegetni.

Konyhanyelven a valszámnak az a megfigyelés az alapja, hogy egy véletlenszerű eseményt (pl. kockadobás) elég sokszor megismételve, az esemény relatív gyakorisága egy konstanshoz közelít, amit az esemény valószínűségének nevezünk. Például egy szabályos dobókocka esetén annak az esélye, hogy hatost dobok 1/6. A kockadobáshoz annak kimenetelét hozzárendelő függvény egy (diszkrét) valószínűségi változó. A fent tanultak segítségével fogalmazzuk ezt meg általánosabban.

Immár a valszámban használatos jelöléssel, az (Ω, ℱ, Pr) mértékteret valószínűségi mezőnek nevezzük, ahol Ω nem üres halmaz (a lehetséges kimenetelek halmaza), ℱ az efeletti σ-algebra (események, ahol az esemény kimenetelek halmaza), és Pr : ℱ → [0, 1] mérték úgy, hogy Pr(Ω) = 1 (a biztos esemény valószínűsége 1). Egy A ∈ ℱ esemény valószínűségét Pr(A)-val jelöljük.

A diszkrét valószínűségi mező ennek egy speciális esete, amikor Ω véges vagy megszámlálhatóan végtelen és ℱ = 𝒫(Ω).

Definíció (valószínűségi változó): legyen (Ω, ℱ, Pr) valószínűségi mező és ξ : Ω → ℝ. Ha

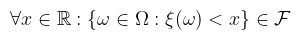
akkor ξ-t valószínűségi változónak nevezzük.

Fent említettem, hogy ez mérhető függvény, konkrétan az a spec. eset, amikor T = { (-∞, x) : x ∈ ℝ }, amiről belátható, hogy (Borel) σ-algebra. Pongyolán mondható az, hogy a v.v. a lehetséges kimenetelekhez olyan értékeket rendel, amiknek a valószínűsége "értelmes" (i.e. jól definiált az integrálás szempontjából).

Valószínűségi változóra alkalmazva valamilyen mérhető f függvényt, szintén v.v.-t kapunk.

A gyakorlatban eltekintünk attól, hogy függvény és csak valamilyen esemény kimeneteléhez rendelt értékként kezeljük. Szemléltető példa (folytonos v.v.-ra) mondjuk a lehetséges hőmérsékletek egy adott napon.

Több valószínűségi változót függetlennek nevezünk, ha a definícióban szereplő halmazaik (mint események) függetlenek, i.e. a metszetük valószínűsége a valószínűségeik szorzata.

Definíció (eloszlásfüggvény): a ξ valószínűségi változó eloszlásfüggvényének az alábbi P : ℝ → [0, 1] függvényt nevezzük: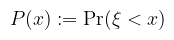


Bár a ξ < x kifejezés a fentiek értelmében egy halmazt jelöl (és emiatt bizonyos irodalmak kapcsos zárójelbe teszik), ettől kényelmi szempontból szintén eltekintünk. Az eloszlásfüggvény így azt mondja meg, hogy mekkora a valószínűsége annak, hogy a v.v. az x értéknél kisebb.

(megj.: az angol szakirodalmak megengedik a ≤-t is, ez annyit változtat, hogy a függvény jobbról lesz folytonos bal helyett)

Definíció (sűrűségfüggvény): a ξ valószínűségi változót abszolút folytonosnak nevezzük, ha létezik olyan p : ℝ → [0, ∞) Lebesgue-integrálható függvény, hogy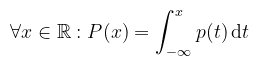


ekkor p-t a ξ sűrűségfüggvényének (probability density function) nevezzük.

Egy fontos dologra felhívnám a figyelmet: a sűrűségfüggvény azt mondja meg, hogy a folytonos v.v. milyen relatív valószínűséggel vesz fel egy adott értéket (azért relatív, mert annak a valsége, hogy egy konkrét értéket vesz fel nulla). A gyakorlatban ez inkább úgy mutatkozik meg, hogy mennyire valószínű, hogy a v.v. egy adott intervallumba esik.

Maradva a hőmérsékletes példánál: annak a valószínűsége, hogy pontosan 16 fok van odakint nulla, de azt meg lehet mondani, hogy mekkora eséllyel esik 15.9 és 16.1 közé. Erre vonatkozik a következő állítás.

Tétel (sűrűségfüggvény tulajdonságai): ha ξ abszolút folytonos valószínűségi változó, akkor minden a, b ∈ ℝ, a < b esetén: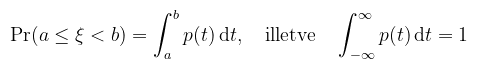


Röviden tehát, ha létezik a v.v.-nak sűrűségfüggvénye, akkor annak a valószínűsége, hogy egy adott intervallumba esik, a sűrűségfüggvény alatti terület azon az intervallumon.

Máshogy megfogalmazva a sűrűségfüggvény az eloszlásfüggvénynek a Lebesgue-mértékre vonatkozó Radon-Nikodym-deriváltja.

Definíció (többdimenziós eloszlás): a ξ = (ξ₁, ..., ξ_n) valószínűségi vektorváltozó közös eloszlásfüggvénye (joint cumulative distribution function) a P : ℝⁿ → [0, 1] függvény: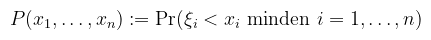


közös sűrűségfüggvénye (joint density function):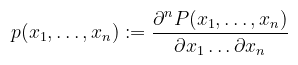


úgy, hogy minden D ⊂ ℝⁿ Lebesgue-mérhető halmazra: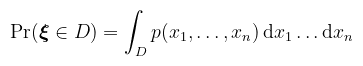


A fogalom kulcsfontosságú szerepet fog játszani a későbbiekben, ugyanis az ún. importance sampling során sűrűségfüggvényeket fogunk keresni, amikből integrálással meghatározva az eloszlásfüggvényt, mintákat (lehetséges kimeneteleket) lehet generálni (például irányokat egy félgömbön belül).

A fogalmak tovább általánosíthatóak, ahol is az eloszlásfüggvény ún. valószínűségi mérték valamilyen μ alapmértékre nézve, ekkor a sűrűségfüggvény szimplán a μ-re vonatkozó Radon-Nikodym-derivált. Ezt külön nem írom le, mert ahogy látni fogjuk, a használt fogalmakhoz (felszín, térszög) elegendő a fenti definíciókat tudni, csak a formulák lesznek rövidebbek.

Definíció (várható érték): legyen (Ω, ℱ, Pr) valószínűségi mező és ξ egy ezen értelmezett valószínűségi változó. A ξ várható értékének nevezzük az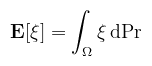


integrált, amennyiben az létezik és véges.

Talán könnyebb megérteni diszkrét esetben, ahol a várható érték a érték-valószínűség szorzatoknak az összege. Megint a kockadobást felhozva példaként, az értékek halmaza { 1, 2, 3, 4, 5, 6 }, egy konkrét érték dobásának valsége 1/6, tehát akkor a kockadobás várható értéke 1/6 · (1 + 2 + 3 + 4 + 5 + 6) = 3.5

A definícióban szereplő folytonos v.v.-ra ez analóg módon egy integrál. De lehet ennél jobbat is mondani:

Tétel (a.f. v.v. várható értéke): amennyiben ξ abszolút folytonos v.v. (létezik sűrűségfüggvénye), akkor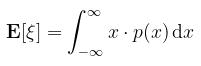


Ez már jobban hasonlít a diszkrét esetre (persze nyilván még mindig integrál). Tudnánk-e valami hasonlót mondani függvényekre (ami integrálközelítésnél segít majd)?

Tétel (az eszméletlen statisztikus törvénye): legyen g a ξ valószínűségi változóra értelmezett mérhető függvény, ekkor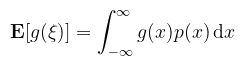


(megj.: ez valószínűségi vektorváltozóra is igaz, ahol p a közös sűrűségfüggvény és többszörösen kell integrálni)

Ezek szerint egy tetszőleges mérhető függvény integrálja tekinthető a függvény várható értékének, amennyiben ismerünk hozzá sűrűségfüggvényt. Ehhez kapcsolódik a várható értéknek egy fontos tulajdonsága:

Tétel (a várható érték lineáris): legyenek ξ₁, …, ξ_n valószínűségi változók és α₁, …, α_n ∈ ℝ konstantsok, ekkor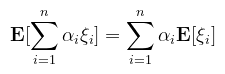


A várható érték ezen tulajdonságai miatt "működik" a Monte Carlo közelítés; a vonatkozó bekezdésben rakom majd ezeket össze.

Definíció (szórásnégyzet): legyen ξ véges várható értékű valószínűségi változó, ekkor ξ szórásnégyzete (variance)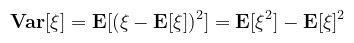


Az egyenlőség a várható érték linearitásából levezethető. A szórásnégyzet pongyolán azt mondja meg, hogy a v.v. értékei mennyire térnek el a várható értéktől.

Megint kockadobásra, E[ξ²] = 1/6 · (1 + 4 + 9 + 16 + 25 + 36) ≈ 15.16, amiből E[ξ²] - E[ξ]² ≈ 2.91

A szórásnégyzet négyzetgyökét nevezzük szórásnak (standard deviation). A fogalom nem hat újdonságként, hiszen a variance shadow mapping keretében már volt róla szó. Ugyanott meg lett említve, hogy az átlag (μ) a v.v. első, a szórásnégyzet (σ²) pedig a második ún. (centrális) momentuma (ne keverjük a korábbi szimbólumokkal).

A variancia jellemzi majd a Monte Carlo közelítés pontosságát: a magas szórásnégyzetű helyeken ún. firefly-ok (fehér pöttyök) jelentkeznek a képen. Az elsődleges cél ezeknek az eltüntetése lesz, különféle mintavételezési stratégiákkal.

Tétel (a szórásnégyzet tulajdonságai): legyenek ξ₁, …, ξ_n független valószínűségi változók és α₁, …, α_n ∈ ℝ konstantsok, ekkor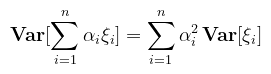


Vigyázat, a függetlenség fontos ennek teljesüléséhez (míg a várható értéknél ez nincs kikötve).

Definíció (peremsűrűség): legyen ξ = (ξ₁, ..., ξ_n) valószínűségi vektorváltozó a p(x₁, ..., x_n) közös sűrűségfüggvénnyel, ekkor a ξ_i valószínűségi változókra külön definiálhatók az ún. peremsűrűségek (marginal density function):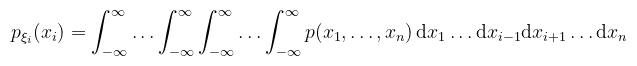


Bár a formula ijesztőnek tűnik, mindössze annyit mond, hogy az i-edik változó szerint nem integrálunk.

A gyakorlatban a kétdimenziós esettel fogok csak foglalkozni, tehát ξ₁ és ξ₂ valségi változók a p(x, y) közös sűrűségfüggvénnyel, ekkor a peremsűrűségek:


A peremeloszlásfüggvények pedig: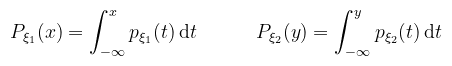


Ez a kétdimenziós inverziós módszernél (később) kap majd szerepet, ahol a félgömb, mint függvény paramétereit v.v.-nak tekintve a peremeloszlásfüggvények inverzéből mintavételezési irányokat állítunk elő. Ehhez szükséges még egy fogalom:

Definíció (feltételes sűrűségfüggvény): legyenek ξ₁ és ξ₂ valségi változók a p(x, y) közös sűrűségfüggvénnyel, ekkor ξ₂ feltételes sűrűségfüggvénye amennyiben ξ₁ már ismert: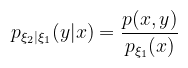


A gyakran emlegetett koszinusz mintavételezés irányait ezen fogalmak segítségével lehet levezetni (ld. lent). Különösen érdekes lesz, amikor bonyolultabb BSDF-ekhez kell mintavételezési stratégiát konstruálni (pl. fénytöréshez).

Először is egy kis motiváció, hogy miért nem jók a klasszikus integrálközelítő módszerek (trapéz szabály, Simpson-módszer, stb.). Ezek ún. hibája (mennyire tér el az integráltól) a felosztás finomságától függ, tehát úgy lehet pontosabb közelítést kapni, ha növeljük a részintervallumok számát (N). Magasabb dimenziókban viszont ez az érték hatványozódik az analóg fogalmakra: 2D-ben már N² minta kell, 3D-ben N³, stb. Amellett, hogy kiszámolni sem egyszerű, a hiba is növekszik.

Ha ez nem lenne elég, alapból egyenletes felosztással dolgoznak, amit az itteni terminológiával naiv közelítésnek nevezünk: fölöslegesen vesz mintát olyan helyekről, amik nem, vagy csak kicsit visznek közelebb az integrálhoz. A cél az lenne, hogy az integrálandó függvény domináns részét meghatározva célzottan helyezzük el a mintavételezési pontokat és ne egyenletesen.

A Monte Carlo integrálközelítés azt mondja, hogy tekintsük a mintákat valószínűségi változónak, valamilyen p sűrűségfüggvénnyel (mostantól röviden pdf). Ezzel egyrészt a dimenzióktól való függés megszűnik, másrészt a sűrűségfüggvényt igény szerint meg tudjuk választani.

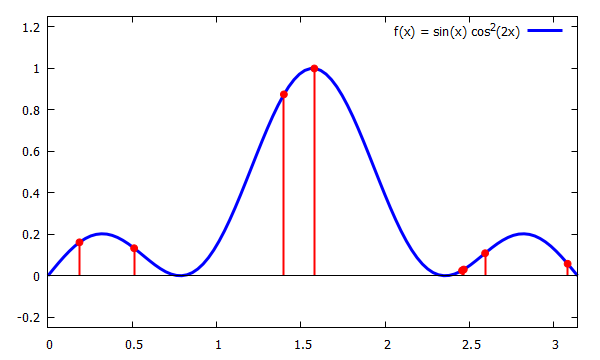
Alapvető különbség, hogy nem érdekel minket, hogy mekkora a távolság a minták (a diagramon piros vonalak) között, csak az érdekel, hogy átlagban igazodjon a választott pdf-hez (pl. egyenletes eloszlás esetén 1/N, ahol N a minták száma).

Ahogy fent megbeszéltük, a diagramon szereplő f függvény (mint v.v.) várható értéke az alábbi integrál: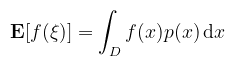


(megj.: nem muszáj végtelenig integrálni, ha nem az a kérdés)

Na oké, de nekünk az f függvény integrálja kellene! Az említett naiv megoldás az, hogy pdf-nek egy konstansot választunk, konkrétan p(x) := 1 / λ(D) és ez felel meg az egyenletes eloszlásnak, ami a folytonos értelemben vett "átlag" fogalom.

Az eredetileg Horvitz-Thompson közelítőnek nevezett módszer erre azt mondja, hogy ha úgyis (nem naiv esetben súlyozott) átlagot számolunk, akkor az integrálközelítő legyen az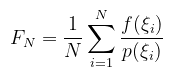


valószínűségi változó, amiről a várható érték tulajdonságai alapján belátható, hogy valóban a függvény integrálját állítja elő: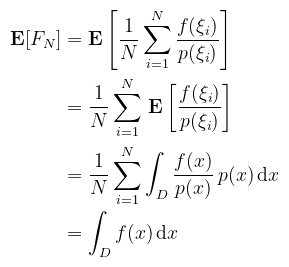


A közelítés érvényességéhez követelmény, hogy a pdf pozitív legyen (nincs negatív valószínűség!), a D tartományon 1-hez integráljon, és ne legyen nulla ott, ahol f nemnulla (ez a GPU implementációban okoz majd némi problémát).

Tétel (a Monte Carlo közelítés hibája): kihasználva, hogy a módszer független v.v.-kkal dolgozik, a szórásnégyzetre az alábbi mondható: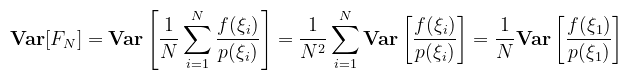


Mégegyszer, ez azért igaz, mert ξ_i-k függetlenek és ugyanabból az eloszlásból valók. Triviális tehát, hogy elég csak az egyik v.v. szórásnégyzetét kiszámolni (legyen csak simán ξ). Jelöljük I-vel az f integrálját D-n, és alkalmazzuk a tanult képleteket: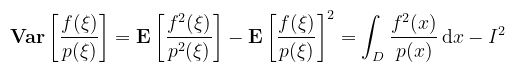


A két egyenletet összerakva azt kapjuk, hogy a szórás (a.k.a. root-mean-square error):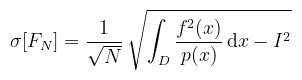


Amiből az látható, hogy a közelítés (átlagos) hibája a minták számának inverz gyökével konvergál nullához. Ez azt jelenti, hogy ha felezni akarom a hibát, akkor négyszer annyi mintát kell vennem. Ez elsőre nem hangzik túl jól, de emlékezzünk, hogy a dimenziók számától független! A path tracing pedig, ha az összes lehetséges útvonalak terét tekintjük, valójában végtelen dimenziós! Egy további erősség a pdf megválaszthatósága (ez a multiple importance sampling-nál fog kibontakozni).

Az alábbi példákban D = [0, π] az integrálás tartománya, az f függvény pedig ami a diagramon szerepel.

Példa (naiv Monte Carlo): vagyis egyenletes eloszlás, azaz p(x) = 1 / π és ez teljesíti is a sűrűségfüggvény feltételeit. A tanultak alapján az eloszlásfüggvény (CDF) és annak inverze kiszámolható: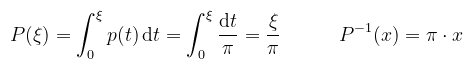


Ez az ún. inverziós módszer, ami folytonos v.v.-k egy mintavételezési technikája: a [0, 1]-beli egyenletes eloszlású v.v.-t áttranszformálja egy másik (itt most a [0, π]-beli szintén egyenletes) eloszlásba.

Az alábbi C++ kód demonstrálja a naiv Monte Carlo közelítést:


A várt eredmény 0.933333333333, de világos, hogy a véletlenszerű természetből adódóan hol alul- hol felülbecsüli. A szórás kiszámolásához egy elég ronda integrált kellene megoldani (parciális integrálás, u-helyettesítés, stb.), szerencsére vannak programok amik elvégzik ezt helyettünk.

A szórás ismeretében (~0.0077) lehet írni egy egyszerű programot, ami a fenti kódot lefuttatja párszor és megmondja, hogy hibahatáron belül van-e az érték (csak az érdekes, hogy átlagosan belül legyen).

Példa (importance sampling): ahogy említettem az egyenletes eloszlással az a probléma, hogy fölöslegesen vesz mintákat olyan helyekről, amik keveset tesznek hozzá az integrálhoz. A cél mindig az, hogy a pdf-et úgy válasszuk meg, hogy az integrálandó függvényből lehetőleg konstans legyen (ekkor a szórás ugyanis nulla). Nyilván ez általában nem tehető meg, de bizonyos domináns részeit el tudjuk tüntetni.

Persze azt is érdemes szem előtt tartani, hogy melyik résznek tudjuk analitikusan kiszámolni az integrálját. Sőt, voltam olyan idióta, hogy cos²(2x)-re kezdtem el kiszámolni, ami szép és jó, csak a CDF inverze nem fejezhető ki elemi függvényekkel (x + sin(x) alakú transzcendens függvény, túlmutat az algebrán).

Marad tehát sin(x), amire gondolkozás nélkül rávágható, hogy p(x) = sin(x) / 2, amiből az eloszlásfüggvény és az inverze: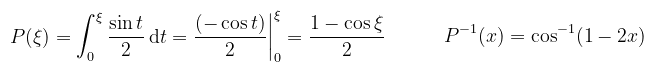


Ami alapján a kód:


Megint segítségül hívva a Desmos-t, látszik, hogy csökkent a szórás (~0.0054). Azt még ki lehet számolni, hogy ha a cos²(2x) tagot ejtenénk ki, akkor mennyi lenne (~0.0047).

Az importance sampling lényege tehát, hogy az integrálandó függvénynek egy olyan részéből csináljunk pdf-et, amit tudunk analitikusan integrálni.

Definíció (torzítás): a Monte Carlo integrálás célja, hogy valamilyen mennyiséget (quantity of interest, Q) közelítsen (jelen esetben Q az integrál értéke) valamilyen F_N = F_N(ξ₁, ..., ξ_N) közelítővel (estimator). A közelítő torzításának (bias) nevezzük a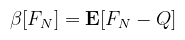


várható értéket. Amennyiben minden N-re a torzítás nulla, akkor a közelítő torzítatlan/elfogulatlan (unbiased).

A fenti levezetésből látható, hogy a Monte Carlo közelítőre ez igaz (i.e. E[F_N] = Q). Ezt azért említem meg, mert egy hibás implementáció könnyen elfogulttá teheti a módszert (pl. ha a v.v.-k nem függetlenek). Ugyanakkor vannak technikák, amik szándékosan bevezetnek torzítást (ún. kvázi-Monte Carlo módszerek) valamilyen kvázi-véletlenszerű sorozattal (low-discrepancy sequence). A cikk végén majd mondok erre néhány példát.

A megjelenítés konkrét fogalmait egyelőre mellőzve, intuitívan menjünk végig a fényforrásokon, illetve a fény-felület interakción. Amikor ránézünk egy fényforrásra, akkor a "fényességét" tetszőleges irányból és távolságból ugyanolyan erősnek érzékeljük. Ami változik az az ún. térszög, ami alól látható (ha messzebb megyek, akkor kisebbnek tűnik).

A térszög tényleg csak ennyi: mekkorának látok egy adott dolgot (fényforrást/objektumot). Amennyiben a 2D-s szögre úgy tekintünk, mint az egységkörből kimetszett körív hossza (radián), akkor analóg módon a térszög az egységgömbből kimetszett felszín (szteradián).

Vetített területnek nevezzük, amikor a térszöget egy objektum vetülete (az egységgömbre) határozza meg, értelemszerűen a távolságától és orientációjától függően.

Persze kicsit bonyolultabb így a helyzet, hiszen a vetületnek könnyen lehet olyan alakja, hogy a tőle függő mennyiségeket csak integrálással lehet kiszámolni. Ez egy kisebb-nagyobb ugrást jelent a matematikai háttérben, ugyanis nem mértékelméleti, hanem differenciálgeometriai oldalról szokás (könnyebb) megközelíteni.

Az ún. felületi integrál valamilyen felület egy paraméterezése szerint értelmezhető. Mivel a megjelenítésben alapvetően térszögekkel dolgozunk, logikus az egységgömb paraméterezését használni:

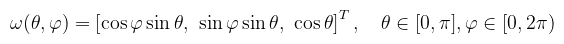
(megj.: a paraméterek sorrendje nem mindegy, én itt az ISO konvenciót használom)

A differenciális térszöget a felületi integrál kapcsán értelmezem, mint azt a végtelenül kicsi felületdarabot, ami szerint az integrálás történik. Pongyolán a felületi integrál definícióját kihasználva valamilyen f teljesen érdektelen függvényre: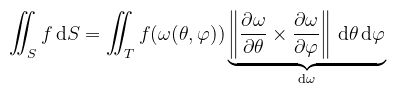


Ahol T most a [0, π] × [0, 2π] síkdarab. A parciális deriváltakat kiszámolva és Wolfram Alpha-ba bepötyögve, a dω-val jelölt értékre az alábbit kapjuk: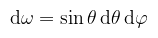


Vizuálisan is lehet értelmezni az egyenlőséget, mint a differenciális szögek által kimetszett négyszög területét, ami a négyszög két oldalának a szorzata. Azért nem így mutattam be, mert a felszín alatt (pun intented) ez nem annyira triviális.

A segítségével viszont kiszámolható például az egységgömb felszíne: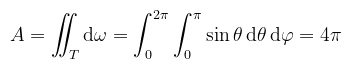


A térszög kapcsán megemlítendő még az egységgömb középpontjától r távolságra levő, n normálvektorú dA felületdarabkára vonatkozó képlet (a fent említett vetített terület/térszög):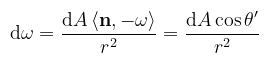


Ezt az azonosságot kihasználva az integrált lehet térszög helyett felszín szerint is venni (ez akkor segít, amikor a fényforrás "kicsi").

Visszakanyarodva a fény-felület interakcióhoz, az, hogy egy fényforrás mennyire tűnik fényesnek, nem mondja meg közvetlenül, hogy milyen erősséggel világít meg valamit. Könnyen demonstrálható egy lapos tárggyal, hogy ha messzebb viszem a fényforrástól és/vagy elforgatom, akkor sötétebbnek tűnik.

A továbbiakhoz még szükséges, hogy a (fél)gömbön (H) belül tudjunk irányokat választani. A Monte Carlo integrálás ugyanis 3D-ben is hasonló recept szerint működik, mint fent, viszont többdimenziós eloszlásokkal. Ehhez kicsit jobban meg kell érteni, hogy az inverziós módszer valójában mit csinál.

Tegyük fel, hogy van már valamilyen ξ valségi változónk, valamilyen p_ξ(x) sűrűségfüggvényből. Alkalmazva rá valamilyen g mérhető függvényt szintén v.v.-t kapunk; kérdés, hogy ez a ζ = g(ξ) milyen eloszlású.

Előfeltétel, hogy g bijektív legyen és tegyük fel, hogy monoton növekvő. Ekkor az eloszlásfüggvény definíciója szerint:

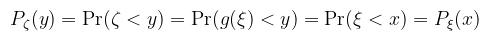
Amiből a sűrűségfüggvényekre a lánccszabály alkalmazásával az alábbi mondható: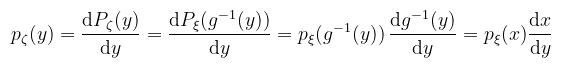


Amennyiben g monoton csökkenő, a jobb oldal negatív előjelű. Általánosan a következőképpen írható fel a egyenlőség: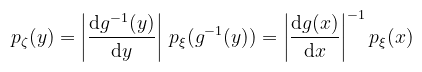


(megj.: ne keverjük, hogy a -1 hatvány mikor jelent inverzet és mikor reciprokot!)

Tehát a sűrűségfüggvényt a g függvény deriváltjának abszolútértékével kell osztani (megfordítottam a hányadost). A levezetés kicsit részletesebben megtekinthető itt (csak annyiban tértem el, hogy egyből kihasználtam a bijektivitást).

A gyakorlatban viszont a sűrűségfüggvények ismertek és a g függvényt (transzformációt) keressük. Az eloszlásfüggvényekre vonatkozó egyenlőségből könnyen látszik, hogy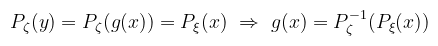


Ami az inverziós módszer általános megfogalmazása; a fenti példákban azt az esetet láttuk, amikor P_ξ(x) az egyenletes eloszlás.

Térjünk most át a többdimenziós eloszlásokra. A közös sűrűségfüggvényekre vonatkozó egyenlőség analóg módon értelmezhető valamilyen T bijektív leképezés Jacobi determinánsa segítségével, ahol most ζ = T(ξ) valószínűségi vektorváltozó: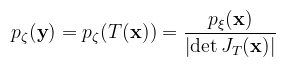


Példaként tekintsük a gömb fent megbeszélt paraméterezését, kiegészítve az r sugárral (i.e. T = r · ω):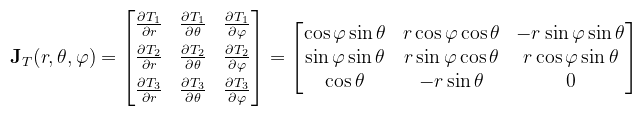


A paraméterek sorrendje még mindig nem mindegy, de most már legalább látjuk, hogy miért nem. A mátrix oszlopainak/sorainak cserélgetése ugyanis a determináns előjelét változtatja (illetve a koordinátarendszer irányítottságát). Mondhatnánk persze, hogy "most úgyis mindegy, mert abszolútértéket kell venni", de a negatív determináns egy kifordított felületet jelent, és pl. a normálvektorok szempontjából az már baromira nem mindegy.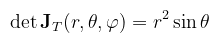


Tegye fel a kezét, aki meglepődött ezen (egyébként így hozható össze dω a Gauss-féle első alapmennyiséggel, ha esetleg vizsgakérdés lenne, mert hát miért is ne lenne az...).

Megadható tehát a sűrűség konverziója Descartes-koordinátarendszerből gömbi koordinátarendszerbe: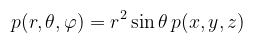


(megj.: az abszolútérték elhagyható, mivel θ ∈ [0, π], és a szinusz ott pozitív)

Itt egy pillanatra álljunk meg, ugyanis az irodalmak kicsit zavarosan viszik tovább ezt az egyenlőséget. Csábító a gondolat, hogy mivel ω-t úgy definiáltuk, mint a gömbfelület pontjait, (x, y, z)-t egyszerűen lecserélhetnénk arra. Csakhogy itt sűrűségekről van szó, amit konkrét pontokra/irányokra nem használhatunk, viszont azoknak egy halmazára már igen.

A helyes eljárás tehát az, hogy egy Ω térszögön vesszük az irányok sűrűségét, amit a p : ℝ³ → [0, ∞) sűrűségfüggvény ír le. Erre viszont a többdimenziós eloszlás definíciója szerint (itt most ω egyben valségi vektorváltozó is):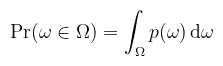


Így már mondhatjuk azt, hogy mivel egy környezetben vettük az irányokat, definiálható egy másik, p : ℝ² → [0, ∞) közös sűrűségfüggvény θ-hoz és φ-hez, felhasználva a fenti felületi integrállal való definíciót: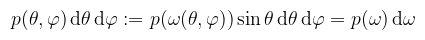


És alkalmazva a dω = sin θ dθ dφ egyenlőséget kapjuk az alábbi Kőbe Vésett Egyenlet™-et: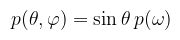


(megj.: gondolom mindenki látja, hogy az egyik p piros, a másik meg zöld)

Ezzel minden készen áll ahhoz, hogy adott p(ω)-hoz az inverziós módszerrel meghatározzuk a θ és φ szögeket, azokból pedig az irányvektort valamilyen ξ₁ és ξ₂ továbbra is [0, 1]-beli egyenletes eloszlású valségi változókra.

Példa (félgömb egyenletes mintavételezése): egyenletes eloszlásnál a pdf konstans, könnyen ki is lehet számolni (1-hez kell integráljon H-n), de intuitívan is meg tudjuk mondani, hogy p(ω) = 1/2π (merthogy a félgömb felszíne 2π).

Úgy kezdődik a buli, hogy peremsűrűség valamelyik változóra (mondjuk θ) és feltételes sűrűség a másikra (az meg akkor φ):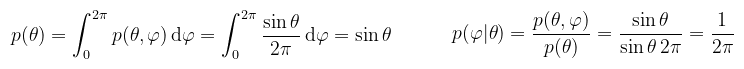


(megj.: azt látjuk, hogy θ és φ függetlenek, azaz valójában nem szükséges feltételes sűrűséget számolni)

Jöhet a peremeloszlás és a feltételes eloszlás: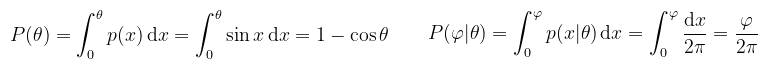


Invertálva ezeket megkaphatóak a szögek: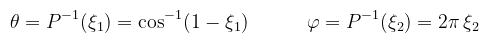


(megj.: ezért kellene alsó index; szintén vizsgához kapcsolódó tanács, hogy nemlétező fogalmakat inkább ne emlegessetek)

Na és most megint álljunk meg, mert ész nélkül kódoltok. Tekerjünk vissza az egységgömb paraméterezéséhez, és a rendkívüli megvilágosodás után lássuk a kódot:


Igen, namost ez a kanonikus bázisban van; értelemszerűen egy tetszőleges normálvektor (mint z-tengely) terébe át kell majd pakolni. Másik megoldás, hogy a bejövő/kimenő vektorokat transzformálod át ide. Én inkább az előbbi mellett döntöttem, mert csak (meg volt már írva).

Nem felejtjük el, hogy a pdf-el mindig le kell osztani (szórakozottságból a kód visszaadja, hogy emlékeztessen), szóval ha ez élesben menne, akkor a közelítést szorozni kell 2π-vel. De.

Példa (félgömb koszinusz mintavételezése): ez a következő bekezdésben nyer majd értelmet, most legyen elég annyi, hogy koszinusszal súlyozott függvényt szeretnénk integrálni. A félgömb aljánál az persze nulla, szóval azon a környéken nem, vagy csak kicsit visz közelebb az integrálhoz. Adódik tehát, hogy ki lehetne ejteni a pdf-el.

Kis számolással ellenőrizhető, hogy a koszinusz integrálja a félgömbön π, tehát p(ω) = cos θ / π megfelel pdf-nek. Mivel láttuk, hogy θ és φ függetlenek, megspórolom a redundáns számolásokat: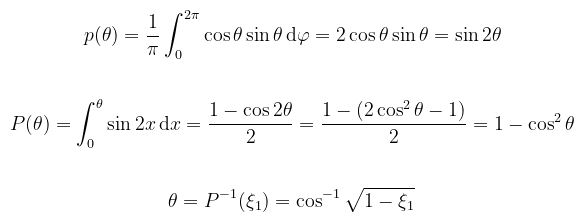


Oké bevallom, ehhez nekem is elő kellett kotornom a függvénytáblázatokat. Meglepő viszont, hogy a mintavételezés kódja csak a négyzetgyökben (és persze a pdf-ben) különbözik a fentitől:


Tényleg meglepő? A könyv részletesebben leírja, de valójában az egységkorong mintavételezését "nyújtottuk ki" egyenletesre, cserébe a félgömbön koszinusz eloszlású pontokat kapva (Malley-módszer). Ennek van egy olyan kellemetlen tulajdonsága, hogy az ún. rétegződést (stratification, értsd pl. multisampling) nem tartja meg. Olyan esetben ugyanez megtehető a Shirley-leképezéssel is (koncentrikus mintavételezés).

Példa (kúp egyenletes mintavételezése): erre még szükség van; ilyenkor θ egy adott θ_max nyitási szögig van értelmezve. Ez az első olyan példa, ahol nem nyilvánvaló, hogy mi a pdf, csak annyit tudunk, hogy konstans.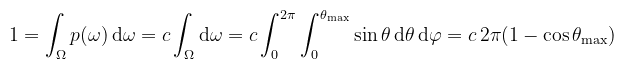


Dehogy bonyolult. Sőt, θ és φ még mindig függetlenek, szóval a közös sűrűség a peremsűrűségek szorzata (de), úgyhogy p(θ)-t fel sem írom külön.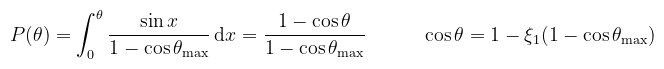


És azonnal írható is át kódba:


Persze ez is a kanonikus bázisban értendő (z-tengely körüli irányok). A könyv elég jól leírja a gyakorlati alkalmazást (gömb által kifeszített kúp mintavételezése), úgyhogy azt nem részletezem (a θ_max nyitási szöget kell kiszámolni és az eredményt átforgatni a normálvektor terébe).

Ha már átforgatás, egy tetszőleges n irányba felettébb egyszerű ezt megtenni (mindegyik itt említett példára):


A kód n körül generál egy ortonormált bázist és átpakolja a v vektort oda. Ahogy mondtam, már meg volt írva, ezért használom (a másik lehetőséget akkor érdemes használni, amikor az adott pontban több mintát veszel egy iteráción belül). Tervezd meg előre, hogy mit szeretnél, és aszerint válassz (a GPU-n nem éri meg eloszlásonként egynél több mintát venni).

Ezt a fogalmat egymástól függetlenül vezette be David Immel és James Kajiya az 1986-os SIGGRAPH-on (igen, már akkor is volt). Ez több mint húsz év a Fred E. Nicodemus által bevezetett BRDF fogalomhoz képest (ne felejtsük el, hogy a 60-as 70-es években még a hadsereg megrendelésére dolgozták ki a később 3D grafikában használt technikákat).

Egy kis retro, hogy akkoriban mit jelentett a grafika (az első mai értelemben vett gyorsítókártya 1999-ben jelent csak meg! Ugyanebben az évben a Star Wars: The Phantom Menace, ami még mai szemmel is látványos CGI). Képzeljétek el egy pillanatra, hogy ezt a sok sületlenséget, amit írok mekkora meló volt akkoriban leprogramozni (gyakran assemblyben).

Na de ne háborgassuk a múltat, inkább röviden ismételjük át a radiometriai fogalmakat (angol nevekkel):

• radiant flux (Φ): közegben egységnyi idő alatt átáramló sugárzási energia
• irradiance (E): egységnyi területre beérkező fluxus
• radiant intensity (I): egységnyi térszögben terjedő fluxus
• radiance (L): egységnyi vetített területre/területről egységnyi térszögben beérkező/elhagyó fluxus

És képletekkel (az időt és a hullámhosszt elhagyva, spectral rendering-gel ugyanis nem foglalkoztam):


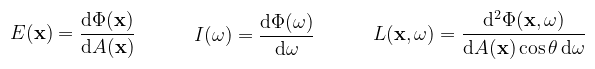
A könyv az egyes differenciálokra mértékként hivatkozik (pl. solid angle measure), de ezt azért teszi, hogy megkülönböztesse a későbbi sűrűségektől (pl. solid angle density). Kicsit pongyola, mert egyébként tényleg mértékként használja ezeket.

Ahogy írtam a radianciát kétféleképpen értelmezzük az ω iránytól függően: beérkező (L_i(x, ω_i)), illetve kimenő (L_o(x, ω_o)). Utóbbit szeretnénk meghatározni, i.e. egy ω_o irányból milyennek látszódik egy adott anyagtulajdonságú felület, amikor egy ω_i irányból érkező fénysugár interaktál vele.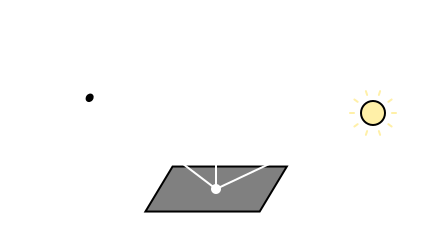


(megj.: az ábráról nem egyértelmű, de természetesen mindegyik vektor normalizált)

A felület által visszatükrözött fény intenzitását az irradiancia határozza meg: ha a felület valamilyen szöget zár be a fényforráshoz képest, akkor a vetített terület jobban szétcsúszik rajta, azaz kevésbé látszik fényesnek.

Valamilyen x felületi pontba az ω_i irány körüli dω_i-vel jelölt végtelenül kicsi térszögből érkező radiancia ((L_i(x, ω_i)) határozza meg a differenciális irradiancát a képletek egyszerű átrendezésével: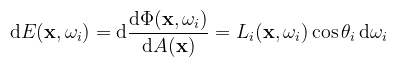


(megj.: vegyük észre, hogy a differenciális irradiancia az iránytól is függ, nem véletlenül!)

Nicodemus azt mutatta meg a dolgozatában, hogy a differenciális irradiancia és a kimenő iránybeli (szenzor által érzékelt) radiancia egyenesen arányos, és ezt az arányt nevezi BRDF-nek (bidirectional reflectance distribution function).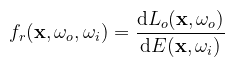


A műszert, amivel ezt a mennyiséget mérik, gonioreflektométernek hívják (lehetetlen megjegyezni); pongyolán úgy működik, hogy az anyagdarab körül a fényforrás és a szenzor egy félgömböt bejárva megméri az összes lehetséges radiancia értéket (és egyéb dolgokat), amiből egy háromdimenziós vektormező áll elő. A MERL adatbázisban több ilyen mérés is megtalálható, ezek megtekinthetőek az azóta open-source BRDF Explorer-rel.

Az anyagtulajdonság leírását ismerve további átrendezéssel, illetve integrálással az alábbi egyenlethez jutunk: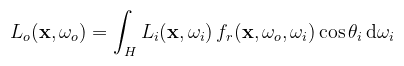


Ahol H az x pont körüli félgömb. Az egyenlet szerint a kimenő iránybeli radiancia a félgömbön belüli összes irányból érkező differenciális irradiancia^* folytonos összege (az integráljel egy stilizált S betű). Logikusan ezért radiance equation a neve.

(* súlyozva a BRDF értékével; ha nem mondok mást, akkor f_r = ρ/π a Lambert BRDF)

Valami azonban még hiányzik: honnan származik a beérkező radiancia? Más szavakkal: hogyan kell módosítani az egyenletet, hogy a fényforrás által kisugárzott radiancia (emitted radiance) is benne legyen? Bármily meglepő úgy, hogy egyszerűen hozzáadjuk: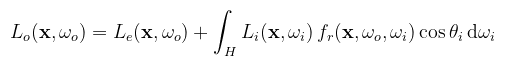


Ami annyit jelent, hogy ha az x pont egy fényforráson van, akkor L_e(x, ω_o) a kisugárzott radiancia. Ha nem fényforráson van, akkor pedig nulla.

Mivel a rekurzivitása által a teljes globális megvilágítást összefoglalja egyetlen formulában, a neve rendering equation.

Fontos még megemlíteni, hogy a differenciális térszög helyébe behelyettesíthető a térszög-felszín összefüggés, ami által az integrálást egy tetszőleges felületen is elvégezhetjük (tipikusan fényforráson):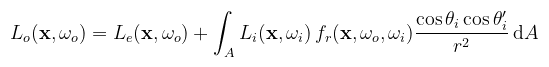


Kétféle mérték szerint is működik tehát az integrálás, lássuk hogyan tudjuk ezt a tudást kamatoztatni.

Ez az első konkrét módszer, amihez példakódot is írtam. Arra a kérdésre keresünk választ, hogy mit kell akkor csinálni, amikor többféle stratégia szerint is mintavételezhetnénk:

Helyhiány miatt csak a lényeget rajzoltam meg. A bal oldali ábrán szereplő matt felületet (a BRDF lufi egy félgömb) alapból koszinusz eloszlással mintavételeznénk, de akkor rengeteg minta nem találja el a fényforrást. Célszerűbb ezért a fényforrás szerint mintavételezni.

A jobb oldali ábrán viszont egy tükröző felület van (a BRDF lufi keskeny), itt meg a BRDF-et éri meg inkább mintavételezni (szélsőséges eset a tökéletes tükröződés, amikor pontosan egy irány van).

Amit Veach megmutatott az az, hogy hogyan lehet ezeket a stratégiákat úgy összekombinálni, hogy a döntéssel igazából ne kelljen foglalkozni. A formális definícióval viszont óvatosan kell bánni, mert különböző irodalmak máshogyan mutatják be.

Induljunk ki abból, hogy továbbra is valamilyen f függvény integrálját szeretnénk közelíteni, viszont most M darab mintavételezési stratégiánk van, amikből összesen N mintát húzunk (egy konkrét p_i pdf-ből N_i mintát). Ekkor a MIS közelítőt az alábbi módon írhatjuk fel: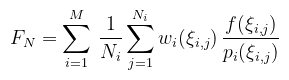


ahol a w_i-k súlyfüggvények az alábbi feltételekkel:

• Σ w_i(x) = 1, ha f(x) ≠ 0
• w_i(x) = 0, ha p_i(x) = 0

Hasonlóan mint fent belátható, hogy ekkor a MIS közelítő torzítatlan, azaz előállítja az f integrálját. Bár Veach több súlyfüggvényt is mutat, bebizonyítja, hogy az alábbinál nem lehet lényegesen jobbat adni:


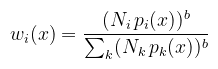
Ami b = 1 esetén balance heuristic, egyébként power heuristic névre hallgat (a gyakorlatban b = 2 jó választás). Ennek a szerepe, hogy azokon a helyeken, ahol egy pdf gyengén teljesít (pl. firefly-t csinál a pixelből), ott a hozzá tartozó értéket lenyomja nullához közelre.

Röviden a példakódról: mivel magát az algoritmust akartam tesztelni, a felhasználható objektumok (itt) analitikus felületek (gömb, síkdarab, stb.), amikkel könnyű metszetet találni. Az implementáció a fragment shader-ben található, hasonlóan mint ahogy korábbi cikkekben is csináltam (a különbség igazából csak a véletlenszám generátor). A shader minden pixelre megkeresi a sugár mentén legközelebbi objektummal való metszetet, meghatározza a szükséges adatokat és meghívja a lenti kódot.

Ja igen, mert amit az ábrákon bemutattam egyébként explicit light sampling-nak nevezik. Eldönthető, hogy minden fényforrást beleveszünk-e a számolásba vagy véletlenszerűen választunk egyet (akár azt is importance sampling-gal). Mindkettőt kipróbáltam, de ennél a példánál az előbbit alkalmazom.

Anélkül, hogy az egyes részimplementációkba belemennék, csak a MIS-re koncentrálva mutatom meg a kód releváns részét. Ha valakit ez nagyon zavar, akkor ahogy mondtam, gondoljon a Lambert BRDF-re (ρ/π, a hozzá való pdf pedig cos(θ)/π). Kétféle mintavételezési stratégia van, mindkettő szerint csak 1-1 mintát veszek (viszont öt darab fényforrásra, szóval összesen hat mintavételezés van).


Rengeteg kérdés merül fel, pedig igyekeztem egyszerűsíteni a kódot. Azt kell észben tartani, hogy ez a GPU-n fut, tehát ha meg tudok spórolni valamit, azt megspórolom. A fények mintavételezésénél például nem érdekel, hogy mi van abban az irányban, ezért a Visibility() egy korán termináló ciklus. A BRDF mintavételezésekor viszont tudnom kell, hogy fényforrást talált-e el és melyiket.

Az is látszik, hogy érdemes mindenféle kombinációt implementálni: olyat ami mintavételez, kiértékel vagy mindkettőt megcsinálja. A pdf-eket célszerű külön függvényként is elérhetővé tenni.

Másfélmillió forintos kérdés, hogy a fényeknél miért van n·l illetve pdf-el osztás, a BRDF-nél meg miért nincs. Azért, mert a SampleEvaluateBSDFImportance(), ahogy a nevében is benne van kiértékeli a BRDF-et a megfelelő importance sampling stratégiát is figyelembe véve (ezzel szintén időt spórol).

Na de lássuk, hogy miben segít ez (mondjuk 4 iterációra):


(megj.: Veach szerint teljesen mindegy, hogy a mintákat hogyan osztod szét, amíg a súlyfüggvényt jól választod meg)

Amint a képen látható (klikk), valóban anélkül kombinálja össze az egyes stratégiák előnyeit, hogy bármit is tudna a jelenetről. A fény mintavételezése például erős kis fényforrások esetén, de gyenge a nagyoknál. Hasonlóan a BRDF mintavételezése nagy fényforrásoknál erős, a kicsiket viszont el se találja. Sőt, mivel csak a BRDF lufin belül mintavételez, a köztes helyeken fekete.

Még egyszer, ezeket a képeket direkt kevés iterációval csináltam (összesen 24 minta). Gondolom nem kell mondani, hogy normális felbontásban és sok iterációra is teljesen valósidejű.

Jöjjön most egy kis kitérő arról, hogy hogyan kell ilyen tükröződéseket csinálni (és miért BSDF szerepel a kódban).

Tulajdonképpen volt már erről szó, de akkor helytelenül Cook-Torrance modellnek írtam (utóbbi π-vel oszt le 4 helyett). Mentségemre az akkori irodalmak is összekeverték. Az egyébként valóban igaz, hogy a Cook-Torrance BRDF egy általánosabb fejlesztés (1982, hol máshol, mint a Lucasfilm-nél), merthogy az eredeti elméletet 1967-ben publikálta K. E. Torrance és E. M. Sparrow. Nosztalgiából érdemes elolvasni, hogy akkor hogyan jutottak el a modellhez. Szerintem nyugodtan mondhatjuk, hogy kiállta az idő próbáját.

Ebben a bekezdésben egyrészt pontosítani szeretnék néhány dolgot, amit a raszter alapú physically based rendering kapcsán hordoztam magammal (az akkori irodalmak javaslatára), másrészt hatékony mintavételezési stratégiákat mutatok be a modellhez.

Az eredeti dolgozat azzal a jelenséggel foglalkozik, amikor a felületről visszatükrözött fény nem az ún. spekuláris irány körül (ahonnan tökéletesen tükröződne) a legerősebb, hanem egy annál nagyobb szögnél. A modellt arra alapozzák, hogy a felület apró, véletlenszerű irányba néző (viszont tökéletesen tükröző) mikrofelületekből áll. Ugyanezért, minél "rücskösebb" egy felület, a tükrözött fény annál mosottasabb.

Mivel a mikrofelületek tökéletesen tükröznek, közülük csak azok járulnak hozzá a makroszkopikus tükröződéshez, amelyeknek a normálvektora ω_h = normalize(ω_i + ω_o) (a félvektor, vektor és tünde utódja). A könyv levezeti, én csak leírom a BRDF-et:

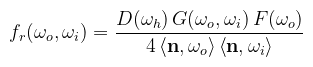
Ahol D a mikrofelület normálvektorok eloszlását jellemzi, G az ún. masking-shadowing function (ez majd érdekes lesz), F pedig a Fresnel együttható. Az első fontos dolog, amit megemlítenék, hogy bár D és G megválaszthatóak, a közelítések konzisztensek kell legyenek. Például mivel maradok a GGX függvénynél, ahhoz a Smith-GGX közelítést kell használnom G-re (ne tudjátok meg mennyit téptem a hajam, mire rájöttem).

Az alábbi képletek közelítések; az eredeti formulák megtalálhatóak az irodalomjegyzékben (de ember legyen a talpán, aki megérti). α mindig a rücskösséget jelenti (nem szabad varacskolni mint raszterizációnál, mert nem fogsz rájönni, hogy mitől rossz):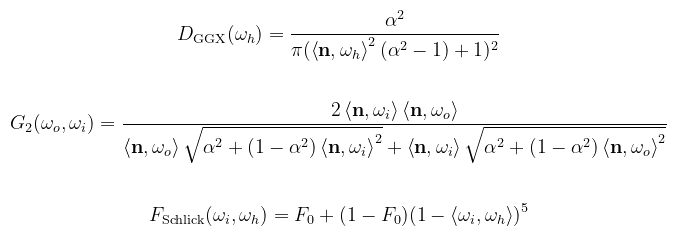


(megj.: G₂-nek helyhiány miatt nem írtam ki a nevét; egyébként height-correlated Smith-GGX)

Ezt így ne kódoljátok le. Persze szükség lesz rá, de a képletből nem látszik, hogy miként kell a GPU-ra optimalizálni. Fontosabb kérdés, hogy hogyan lehet mintavételezni. Először is nézzük meg, hogy a három részfüggvény közül melyik a domináns:


(megj.: G₂-ben az a sötétebb rész a képletből következik, a BRDF nevezője ejti ki)

Ha nem gondolkozunk sokat, akkor az látható, hogy a D függvény határozza meg a BRDF lufi alakját. Az ilyen függvények kollektív elnevezése NDF (normal distribution function), és definíció szerint azt mondja meg, hogy mennyire "valószínű", hogy a mikrofelület a paraméterben megkapott irányba néz (i.e. egy Dirac delta eloszlás integrálja a mikrofelszínen).

Itt most egy kicsit makizni fogok, de az NDF-nek van egy olyan tulajdonsága, hogy a mikrofelszín vetített területe a makrofelület normálvektora mentén meg kell egyezzen a makrofelület területével (konvenció szerint 1 m²). Formálisan: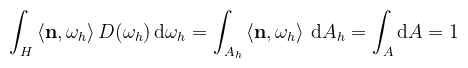


Ahol dA_h azoknak a mikrofelületeknek az összterülete, amiknek a normálvektora a dω_h térszögbe esik (makizás, mondom). A levezetés megtalálható Eric Heitz publikációjában (erre G₂ kapcsán majd még visszatérek).

A lényeg, hogy a felírt integrandus teljesíti a pdf követelményeit. Sőt, mivel izotróp (forgatás hatására nem változik a kinézete), θ és φ megint függetlenek. A skaláris szorzat írható cos θ_h-ként is, tehát akkor a Kőbe Vésett Egyenlet™ alapján a GGX függvényre: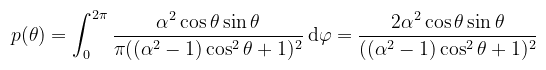


Naja, hát ez nem valami szép; mázlink van viszont, mert u = cos² x helyettesítésssel: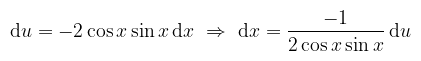


Ez tök jó, mert kiejti a számlálót. Ne felejtsük el viszont, hogy az integrálás tartományát is le kell követni: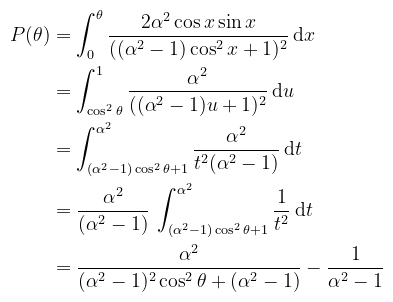


Baromi könnyű elszámolni, különösen az előjelváltásoknál. Láthatóan kellett egy második helyettesítés is; a kettőt össze lehetett volna vonni, mindegy (ne csak én számoljak). A mintavételezéshez ezt még ugye invertálni kell; a hajtépés elkerülése érdekében csak az eredményt írom le: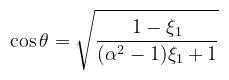


Egyszerű algebrai manipulációkat kellett csak alkalmazni (viszont hosszú leírni). Lássuk akkor, hogy kódban hogyan fest:


És most ismét álljunk meg. Mire kapunk itt mintát? A változónév árulkodik: a félvektorra. Ezt nagyon nem szabad elfelejteni, mert szintén nem fogsz rájönni, hogy miért nem úgy néz ki, ahogy kellene. A bejövő irányt tehát a félvektorból és a kimenő vektorból kell visszaszámolni.

Na de várjunk...ha az irányok különböznek, akkor a sűrűségek is! Ha mondjuk θ_h most a félvektor és a kimenő vektor közötti szög, akkor θ_i = 2θ_h (a félvektor definíciójából). Ismét előkapva a függvénytáblákat: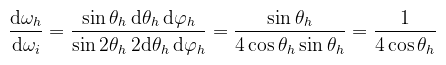


Az irodalmak szerint ez a vektorra való tükrözés Jacobi determinánsa (elhisszük).


Örülünk, Vincent? Nos...igen is, meg nem is. Bár találtunk egy mintavételezési stratégiát, a szépséghiba csak annyi, hogy nem ez a legjobb. Teljesen megfeledkeztünk ugyanis a masking-shadowing függvényről. A mikrofelületek takarásban lehetnek akár a fény (shadowing) akár a kamera szemszögéből (masking). Utóbbi az érdekes: hatékonyabb a közelítés, ha eleve csak a látható mikrofelületek szerint mintavételezünk. Itt térnék vissza Heitz dolgozatához.

Először egy kis fejtágítás: a fenti G₂ az ún. height-correlated masking-shadowing function, ami figyelembe veszi, hogy egy adott mikrofelület magassága korrelációban van a környezetében levőkkel. A Smith mikrofelszín profil ezzel eredetileg nem foglalkozik, hanem egy G₁-el jelölt függvénnyel jellemzi a mikrofelületek adott irányból való láthatóságát. A GGX eloszlásra ez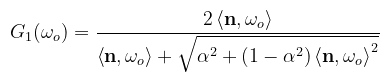


(megj.: vigyázat, nem írtam el, az ott tényleg plusz; speciel két ilyen szorzata a korrelálatlan G₂)

Heitz megmutatja, hogy ezzel az egyirányú G₁ függvénnyel beszorozva adható egy D_ωo-val jelölt függvény, ami immár a kimenő irányból látható mikrofelületek normálvektorainak sűrűségfüggvénye: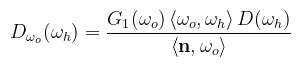


És ez az a pont, ahol a dolgozat kiegészítő része átmegy nehezen érthetőből kénköves pokolba, ugyanis az eloszlásfüggvényre nincs zárt formula (GGX esetén, ahogy ők paraméterezik).

Szerencsére 2018-ban a szerző adott egy jóval egyszerűbb megoldást. Az alapötlet az, hogy α = 1 esetén a GGX lufiból egyenletes eloszlású félgömb lesz (helyettesíts be). Heitz azt mondja, hogy mivel a GGX függvény a nyújtásra nézve invariáns, a számolás elvégezhető úgy, hogy a bejövő vektort megnyújtjuk α-val. Ezáltal dolgozhatunk a félgömbbel, majd az eredményt visszanyomjuk az eredeti lufiba.


Néhányszor átolvasva a dolgozatot nagyjából megérthető, hogy mi történik: a félgömb alapkorongját két félkorongra bontja (az egyik az alapsíkban, a másik a kimenő vektor síkjában). A mintavételezés a félkorongoknak a kimenő irányvektor menti vetületén történik (ld. a dolgozatot ábrákhoz).

Végül nézzük meg, hogy ezzel a mintavételezéssel hogyan egyszerűsödik a tükröződési egyenlet Monte Carlo közelítése: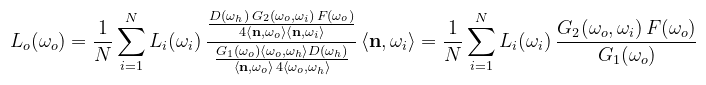


Kiesett D is és a koszinuszok is, ami lényegesen csökkenti a szórást (egy mezei koszinusz mintavételezéshez képest). Pudingpróba 16 minta/pixelre: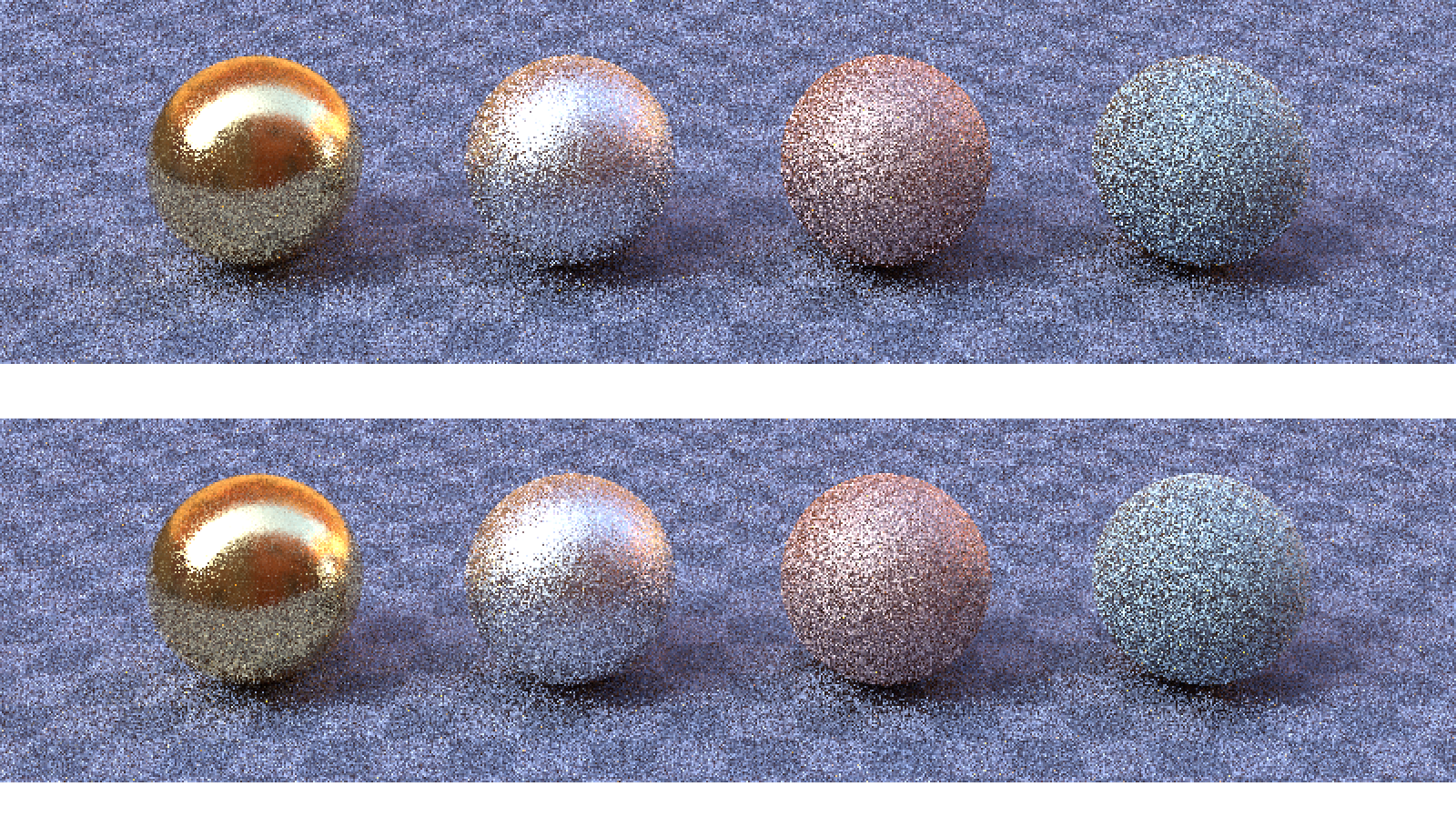


(megj.: mindegyik gömb fém, a rücskösségek balról jobbra: 0.05, 0.25, 0.5, 0.75)

Az látszik, hogy a látható normálvektorokat figyelembe vevő mintavételezés inkább az erősen rücskös felületeknél segít, illetve az objektumok széleinél (ahol éles szög alól látszanak a mikrofelületek). Hozzátenném azért, hogy itt egyéb dolgok is működnek a háttérben, amik csökkentik a szórást, de azok nélkül ilyen kevés iterációra értelmezhetetlen lenne a kép.

Ez elsőre nem nyilvánvaló, merthogy a Fresnel-egyenletek szerint a radiancia egy része tükröződik (BRDF félgömb), a másik része megtörik és áthalad a felületen (BTDF félgömb). Path tracing-ben nem akarunk egyszerre két irányba pattogni. Hogyan lehetne akkor ezt megoldani? Nézzük meg mit csináltunk raszterizációnál, hátha ad ötletet:

(megj.: η = η₁ / η₂ a két közeg törésmutatóinak hányadosa)

Hmm... F és 1 - F? Ezek szerint a Fresnel együttható alapján eldönthető, hogy merre menjünk tovább (és emiatt része lesz a pdf-nek). A BTDF-et viszont még nem tudjuk, ehhez megint a könyvet kell elővenni: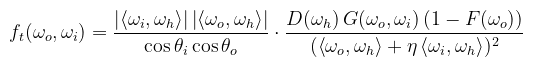


(megj.: vigyázat, a félvektor itt ω_h = ω_o + η ω_i)

Ez még rondább képlet, mint a tükröződés...reménykedjünk, hogy a pdf megint kiejti a dolgokat. Naná, ha megnézzük a könyv levezetését, akkor nyilvánvaló, hogy ki fogja ejteni, ugyanis a BTDF-et a fénytörés Jacobi determinánsával definiálta: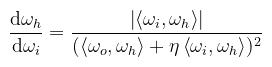


Na most az a helyzet, hogy erre egyik irodalom sem mutat normális bizonyítást. A legközelebbi, amit találtam Jos Stam dolgozata (Appendix B), de amellett, hogy kissé obfuszkált, az eredmény sem egészen az, amit vártam.

Mindegy, lássuk mihez lehet ezzel kezdeni. Természetesen még mindig a látható mikronormálokat mintavételezzük, tehát a Heitz-féle D_ωo-ból kapjuk a félvektort. Viszont ahogy a bekezdés elején mondtam, a Fresnel együttható szerint kell eldönteni, hogy tükröződés vagy fénytörés történt-e:


Ez egy összevont kód, a tényleges implementáció egyéb okokból szét van bontva. A teljes belső visszaverődést (total internal reflection) itt nem kezeltem le; ez olyankor történik, amikor a bejövő sugár az ún. kritikus szögben találja el a felületet (a nagyobb törésmutatójú közegből a kisebb felé) és nem képes áthatolni rajta. Ezt a refract függvény úgy jelzi, hogy nullvektort ad vissza. Az implementációk ilyenkor többnyire terminálják a path-ot.

Egy ehhez kapcsolódó fontos dolog, hogy a BTDF ezek szerint nem szimmetrikus: amikor a kamera irányából számoljuk a fénytörést, akkor az eredményt be kell még szorozni η²-el (ld. a könyv vonatkozó részét). A referencia ezt mikrofelületnél valamiért nem teszi meg (úgyhogy értelemszerűen kihagytam).

Ha ismét összerakjuk az egyes képleteket, akkor kiértékeléskor a BTDF az alábbira egyszerűsödik (nem fért ki, de elhiszitek):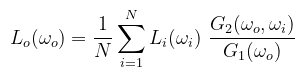


Igen, tényleg ennyi. Ha kicsit belegondolunk annyira nem meglepő: mivel a Fresnel együtthatót belevettük a mintavételezésbe (és ezáltal a pdf-be), logikus, hogy eltűnt a kiértékelésből. A BTDF pedig a megfelelő vektorok megfordításával teljesen hasonló, mint a BRDF (kivéve az említett asszimetriát). A kettőt együtt BSDF-nek (bidirectional scattering distribution function) nevezzük.

Az alábbi képet hagytam végigkonvergálni (1024 iteráció, néhány másodperc):


(megj.: üveggömbök, azaz η = 1.5; a rücskösségek balról jobbra: 0.005, 0.05, 0.1, 0.25)

Színes üvegeket eddig nem sikerült értelmesen megjelenítenem (és ez nem csak nálam probléma). A tesztjelenetek is inkább ködösítő közegekkel oldják meg, maga az üveg színtelen. Miközben mutogattam ezt a képet felmerült az a kérdés, hogy mi az ott a gömbök alján: a kétszeres fénytörés lencsehatást vált ki, szóval az a háttér (illetve az environment map amit éppen beraktam).

Gondolom világos, hogy fénytöréshez már tényleges path tracing-re van szükség, szóval itt is megelőlegeztem néhány dolgot.

Ebben a bekezdésben arra szeretnék fókuszálni, hogy mi is ez a "standard" megközelítés fotorealiszikus képek előállítására. Röviden mondhatnám azt, hogy "amit könnyű leimplementálni", ami egyébként igaz, amennyiben a fenti speciális BSDF-eket figyelmen kívül hagyod. De akkor kénytelen vagy arra hagyatkozni, amit már ismersz (pl. a sokat emlegetett Lambert BRDF). Egyébként nem tévednél (csak vizuálisan egyhangú lenne a kép).

Nézzük végig, hogy mikkel foglalkoztunk eddig: volt először a (mintavételezés szempontból) naiv megközelítés, amikor egyenletes eloszlással "próba-szerencse" alapon próbáltuk közelíteni valamilyen függvény integrálját.

Jött utána az importance sampling, ami már az integrandus egy domináns részét sűrűségfüggvénnyé alakítva csökkentette a szórást (így az integrál értéke már kevesebb iteráció után előállt).

Ezt továbbgondolva Veach dolgozata alapján eljutottunk a multiple importance sampling-hoz, amit a megjelenítési egyenletre alkalmazva megkaptuk a közvetlen megvilágítást (direct lighting). Mellette megtanultuk a BSDF hatékony mintavételezését (Heitz).

Most ott tartunk, hogy a közvetlen megvilágítást már ki tudjuk számolni, viszont a BSDF-ek ismeretében világos, hogy ez nem lesz elég: tovább kell pattognunk (tükröződéshez, fénytöréshez). Ki lehet egészíteni az implementációt úgy, hogy ahol van értelme, ott a BSDF-ből mintavételezünk egy új irányt és hasonlóan kiszámoljuk a közvetlen megvilágítást. De akkor miért ne oldanánk meg magát a megjelenítési egyenletet?

Az implementáció kapcsán a Veach által kidolgozott útintegrál megfogalmazást fogom bemutatni. A fogalom ismerős lehet kvantummechanikából Richard Feynman és a kétrés-kísérlet kapcsán, de némi utánajárással arra a következtetésre jutottam, hogy csak retorikailag, illetve alapötletben egyeznek. Az itteni path tracer implementációk nem alkalmasak kvantummechanikai jelenségek demonstrálására.

Könnyítésként (és az irodalmakkal való konzisztencia miatt) a jelölést lecserélem pontokból álló láncokra, tehát például a p₁ pontból a p₀ pontba érkező radianciát így fogom jelölni (amennyiben látható egyik a másikból):

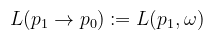
Hasonlóan, ha adottak az ω_i és ω_o irányok, akkor a p₂, p₁, p₀ pontsorozatra hasonlóan jelölhető a BSDF, illetve a térszögből felszínbe való konverzió Jacobi determinánsa, amit az irodalmak egyszerűen csak G-vel jelölnek (geometry term). Ezt külön nem írom le, mert már láttuk (a két koszinusz szorzata osztva a távolság négyzetével és beszorozva egy láthatósági függvénnyel).

A megjelenítési egyenlet (vagy most már akkor inkább fényterjedési egyenlet) a következőképpen írható fel: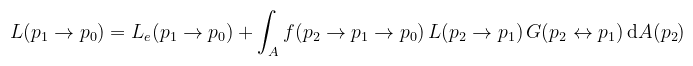


A félreértések elkerülése végett mégegyszer: ez a megjelenítési egyenletnek egy másfajta felírása, amiben az irányok ki vannak cserélve erre az ún. "hárompontos alakra". A rekurziv jellegét természetesen megőrizte: az integrandusban szereplő radiancia helyén lehet "pumpálni".

Kezdjük el akkor az egyenlet kifejtését: vegyünk egy negyedik pontot (p₃), és az arra felírt teljesen hasonló egyenlet jobb oldalát helyettesítsük be L(p₂ → p₁) helyére (katt a nagyításhoz):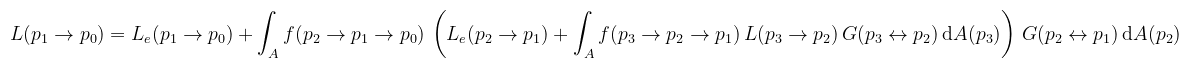


Gondolom nem kell mondani, hogy ezt milyen melós dolog újra meg újra elvégezni (egyre hosszabb formulát kapva), úgyhogy az algebrai manipulációkat rátok bízva a kompakt alakot adom meg: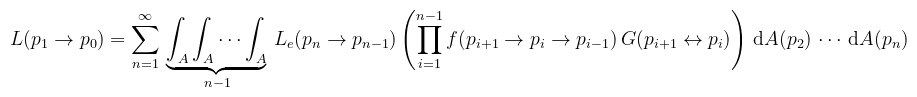


Megjegyzendő, hogy n itt az útvonal hossza. Lehetne kötekedni, hogy a formula kicsit csal, de ha nem integrálunk (n = 1), akkor értelemszerűen a mértéket sem kell odaképzelni. Amikor path tracing-ről beszélünk, akkor p₀ mindig a filmen/lencsén értendő, p_n pedig egy fényforráson.

Az útintegrált (jobb fordítás híján) az ún. útvonaltéren (path space, Ω) értelmezzük, ami az összes n hosszú útvonalak halmazainak úniója (tehát minden lehetséges véges útvonal). Vegyük észre, hogy ebben már nincs rekurzivitás.

A p = p₀, ..., p_n alakú útvonalakra definiáljuk az alábbi mértéket (ún. area-product measure, i.e. területek szorzata):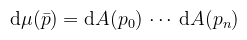


(megj.: miért differenciál: azért mert magát a mértéket halmazokra lehet definiálni)

És ami maradt az akkor ezek szerint az integrandus, vagy becsületes nevén measurement contribution function, szintén n hosszú útvonalanként értelmezve, azaz a szumma lecserélődik integrálra, és az alábbi egyenletet nevezzük útintegrál megfogalmazásnak: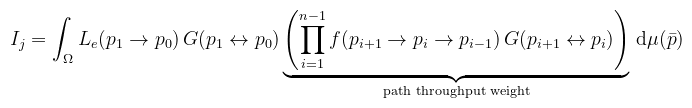


(megj.: I_j a j-edik pixelre kapott mérés; kicsit önkényesen definiáltam, de ugyanez az irodalmakról is elmondható)

Ami tehát az említett absztrakt útvonaltéren vett integrál, amiben maguk az útvonalak tekinthetőek pontoknak. Több előnye is van ennek a felírásnak, amit a haladó algoritmusok ki is használnak (pl. az útvonalakat lehet mintavételezni). Részletesebben ld. a SIGGRAPH prezentációját. Most egyelőre elég lesz az, hogy a Monte Carlo közelítését átírjuk shader-be.

Az implementáció előtt nézzünk képeket (256 iteráció, legfeljebb 15 hosszú útvonalak):


(megj.: a fenti útintegrál alak Monte Carlo közelítése a középső kép, tehát a naiv path tracing)

Az útvonalakat az ún. local path sampling nevű módszerrel állítom elő, a kamerából kiindulva. Az útvonal (mostantól path) következő pontja az aktuálisan eltalált felület BSDF-jéből választott irány mentén való következő metszéspont. A "naiv" szó itt arra utal, hogy ilyen módon pattogtatva a sugarat reménykedek, hogy eltalálja a fényforrást (implicit path). Ne zavarjon meg az elnevezés, mert egyébként minden ismert importance sampling stratégiát alkalmazok!

A next event estimation nevű technika alatt annyit kell érteni, hogy az útintegrál alakba minden pattogásnál belevesszük a közvetlen megvilágítást is (i.e. meg kell hívni a SampleLightsExplicit() függvényt). Logikusan ezért szokták úgy is mondani, hogy path tracing with explicit light sampling, de szerintem ez egy kicsit félrevezető elnevezés: tévesen lehet úgy értelmezni, mintha az első két képet összeadnám (nem!). Ellenben érdemes összevetni, hogy milyen röhejes mértékben csökkenti le a szórást! Ez akkor látszik jól igazán, amikor a fényforrás "kicsi".

Felmerül viszont egy kérdés: mégis meddig érdemes pattogtatni a sugarat (szintén naiv dolog lenne azt feltételezni, hogy majd csak kiszökik egyszer a jelenetből)? Az a nagy helyzet ugyanis, hogy ha fix számú pattogást engedek meg, az torzítja a közelítést (viszont elég sok iterációval kompenzálható). Erre a Russian roulette nevű technika ad megoldást, ami egy adott pattogásszám után véletlenszerűen terminálja a path-ot.

Természetesen ezen orosz rulettre is alkalmazható importance sampling: ha a pattogások által összegyűjtött indirekt megvilágítás (throughput) nem növekszik lényegesen (i.e. egy véletlenszerű értéknél kisebb), akkor a path-ot korán terminálom (ld. Veach dolgozatát a formális levezetéshez).

Az alábbi kód a next event estimation-nel és a Russian roulette-tel kiegészített TraceScene() függvény (szintén zanzásítva):


Ebben a kódban a fényforrásokat és az objektumokat is ugyanazzal a struktúrával reprezentálom, a fényeket külön megjelölve (és akkor a BSDF alapszíne a radiancia). Ez shader-ek esetén mindig kényelmi ok: elég egy buffert megadni, ami (ha a GPU is úgy gondolja) akár egyben befér a cache-be. A fényforrások a buffer elején vannak, szintén kényelmi okokból.

Arra érdemes odafigyelni next event estimation esetén, hogy ha a path mégiscsak eltalálja a fényforrást, akkor nem szabad hozzáadni a radianciát, hiszen a közvetlen megvilágításban már benne van (ún. double dip). Kivétel természetesen az elsődleges sugár és az olyan path-ok, amik fénytörés után jutottak ide (a kausztikákra ugyanis nem lehet közvetlen megvilágítást számolni). Hasonló igaz Dirac delta BSDF-ekre is (tökéletes tükröződés/fénytörés).

Az eddigi képeken analitikus felületeket jelenítettem meg, azokkal ugyanis gyorsan lehet metszetet találni, ezáltal lehet a konkrét algoritmusokra koncentrálni. Tetszőleges modell megjelenítése viszont már nem ennyire triviális; legrosszabb esetben az összes modellt alkotó háromszöggel való metszést tesztelni kell, ami nyilvánvalóan nem járható út.

Szükség van tehát valamifajta térpartícionálásra. A szakirodalmak alapján a bounding volume hierarchy (BVH)-ra esett a választásom, de implementációfüggő, hogy mennyire hatékony. Megemlítendő, hogy a hardveres ray tracing-et támogató kártyák alapvetően a térpartícionáló gyorsítóstruktúrát csinálják meg, illetve kezelik hatékonyan (szintén implementációfüggő, hogy milyet).

A BVH bináris térpartícionálás, kiindulásként megkapja a teljes jelenet befoglaló dobozát, majd valamelyik kanonikus irány mentén kettévágja valamilyen heurisztika által megadott helyen. Ezt rekurzívan tovább csinálja az így kapott kisebb befoglaló dobozokra, amíg el nem ér valamilyen terminálási feltételt.

A konkrét algoritmus szemszögéből a modell egy háromszögleves, tehát nem tud mást csinálni, mint minden háromszögnek (igen) kiszámolja a befoglaló dobozát. A vágási pont megkeresése úgy történik, hogy az aktuálisan szétvágandó dobozt felosztja valahány potenciális vágósíkra, és mindegyikre megnézi, hogy a tartalmazott befoglaló dobozok attól "balra" vagy "jobbra" helyezkednek-e el (majd ezekből kiszámol egy "bal" és "jobb" befoglaló dobozt). A vágósíkok közül végül azt választja ki, amelyikre az ún. surface area heuristic minimális. Ezzel azt tudja garantálni, hogy egyrészt a partícionálás a lehető legjobban illeszkedik a modell egyes részegységeire (pongyolán, ahol a háromszögek sűrűsége nagy), másrészt csak arra folytatja a rekurziót, amerre tényleg szükséges. Más térpartícionáló algoritmusokkal szemben a vágósíkra eső háromszögeket nem kell szétvágni.

A leírtakból gondolom világos, hogy a BVH előállítása rendkívül időigényes, szóval az elkészülése után kiírom a merevlemezre. Hardverlimitáció miatt a fa maximális magasságát 32-re korlátoztam, de az ügyes heurisztika miatt még viszonylag nagy modellek esetén (1-2 millió háromszög) sem lépi túl (persze ennél nagyságrendekkel nagyobb modelleket is tud kezelni, csak diavetítő lesz az eredmény).

(megj.: a bal oldali kép azt mutatja, hogy a bejárás hol megy mélyebbre a fában; a jobb oldali képen maga a fa látható)

A hardverlimitáció az, hogy a GPU-n nincs hagyományos értelemben vett stack: GCN architektúrán work item-enként 4096 temporáris vektorregiszter áll rendelkezésre, és abba minden bele kell férjen (tehát nem csak a BVH bejárása, hanem az összes fenti számolás is). Ez erősen korlátozza, hogy mit lehet cache-elni az osztott illetve a privát memóriában (az anyagokon és fényeken kívül gyakorlatilag semmit). Ennek az eredménye iszonyatos mennyiségű cache miss lesz, mivel az egyes work item-ek folyamatosan konkurens módon nyúlkálnak a globális memóriába (szerencsére csak olvassák).

A képen látható elsődleges sugárvetés egyébként még erre a bonyolult modellre is stabil 60 fps; akkor kezd el meredeken zuhanni, amikor elkezdem a konkrét sugárkövetést (az viszont már modellmérettől függetlenül lassú az említett cache miss-ek és a dinamikus elágazások miatt).

A kódból a BVH iteratív bejárását mutatom meg (a stack hiánya miatt rekurzió sincs):


(megj.: a RightOrStart tagváltozó felső két bitjében tárolom a vágás tengelyét)

Bármelyik a témával foglalkozó irodalom hasonló kódot fog mutatni, szóval ezt nem én találtam ki. Kitaláltam viszont mást, ugyanis ez a kód mindig a kamerához legközelebbi metszési pontot adja meg (closest hit), holott például láthatósági teszthez elég lenne csak egy metszetet találni (any hit). Itt jelenik meg az első hasonlóság a hardveres sugárkövetéssel, ott ugyanis külön van closest hit shader és any hit shader (ugyanezen ok miatt).

Az any hit esetén viszont van egy bökkenő: bizonyos esetekben újra invokálni szeretném, hogy folytassa a keresést. Ez olyankor jön elő, amikor a jelenetben ún. null-interakciókat is megengedek (pl. átlátszó objektumok vagy ködösítő közegek). Ezeknél ugyanis bár talált metszetet, nem számítanak blokkolónak (átengedik a sugarat). A tesztmodellben ilyen például a függöny.

Utóbbi algoritmus tehát állapotfüggő; ezt úgy hidaltam át, hogy a stack-et és az egyéb szükséges dolgokat kiszerveztem egy külön BVHTraverseState nevű struktúrába, amit mindig megkap paraméterben. Maga a bejárás egyébként teljesen hasonló, annyi különbséggel, hogy ha talált metszetet, akkor azonnal visszatér.


(megj.: a jobb oldali kép validálva van a Mitsuba illetve a pbrt-v3 programokhoz)

Érdekességképpen megemlítem, hogy bár a bal oldali kép tisztán fehér diffúz felületekből áll, az előállítása jóval lassabb, mint a tényleges jelenetre ráengedni az algoritmust. Ez elsőre viccesnek hangzik, de gondoljunk bele, hogy a Lambert BRDF-et szinte a teljes félgömbben mintavételezzük (így rengeteg új lehetséges irány van), míg a valódi jelenetben a BRDF-ek "egyszerűek", akár a GGX-el árnyalt bútorzat, vagy a tükrök, ahol csak egyetlen lehetséges irány van (ún. Dirac delta BSDF).

Külön nem mutatom be, de a bútorzatnál az Ashikhmin-Shirley BRDF-et használom, ami az energiamegmaradást megtartva modellezi a "lakkozott" (a diffúz felett egy vékony dielektrikus réteg) felületeket. A könyvben ezt FresnelBlend néven lehet megtalálni. A Mitsuba és a Tungsten egy másik modellt használ, de a nemlineáris hatásokat kikapcsolva ugyanazt az eredményt adják. Nem árulják el, de szerintem ez a Weidlich-Wilkie BRDF. Az előre kiszámolt konstansokkal kipróbáltam, és stimmel (viszont általánosságban több munkát igényel).

Az említett local path sampling nem tesz megkötést arra, hogy hogyan építed fel a path-ot. Például nem muszáj a kamerából indulni, lehet a fényforrásból is (akkor viszont bajban leszel, hogy a filmen hova kell leképezni a pontot, azaz nem kimondottan shader barát). De megtehető az is, hogy generálok egy t hosszú subpath-ot a kamerából, egy s hosszú subpath-ot a fényforrásból és a kettőt egy láthatósági teszttel összekötöm.

...meg ahogy azt a Móricka elképzeli. Ha csak ennyit tennék, akkor kb. soha nem találna kapcsolódási pontot. A bidirectional path tracing (BDPT) ennél sokkal robusztusabb (és elegáns megoldás): a camera subpath minden pontját megpróbálja összekötni a light subpath minden pontjával. Ezt már igen nehéz egyben tesztelni, szóval az első dolgom az volt, hogy az egyes összekötési stratégiákat (amik a lenti piramist alkotják) kimentettem a Mitsuba-ból és egyesével validáltam őket a saját implementációmhoz.

A könyv szóhasználatával: a kamerából induló path-ot nevezzük radiance transport-nak, a fényforrásból indulót pedig importance transport-nak (hiába fordítva lenne logikus). Továbbra is a fenti útintegrál alakot használva az útvonalak most ilyen alakúak:

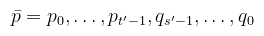
(megj.: a p_i pontok tartoznak a camera subpath-hoz, a q_i pontok a light subpath-hoz)

Ahol t' ≤ t és s' ≤ s. Az említett filmre való nehézkes leképezés miatt az implementációban t ≥ 2, tehát a kamera útvonalán mindig van legalább egy metszési pont (és a kamerával sosem próbálok meg összekötni). A két subpath hosszának variálásával különféle mintavételezési technikákat kapunk, amiknek az összege állítja elő a végleges képet.


(megj.: az s = 0 képek felelnének meg a naiv path tracing-nek, azaz a BDPT egy általánosítása az eredeti algoritmusnak)

Hmm...mintavételezési technikák (súlyozott?) összege...ismerős nem? Ez volt a multiple importance sampling. De vajon mit kell érteni alatta ebben az esetben? Vagy inkább: hogyan kell súlyozni az egyes stratégiákat, hogy a szórás csökkenjen? Mindenki kapaszkodjon meg amibe tud...


Szóval ahhoz, hogy a MIS súlyt ki lehessen számolni, meg kell határozni az adott path-hoz tartozó összes hipotetikus összekötési stratégia pdf-ét. Bár elkezdtem implementálni, végül feladtam, ugyanis rendkívül bonyolult és csak tovább lassítja a már egyébként is rengeteg számolást végző algoritmust. Amennyiben implementálva lenne, akkor a szórást csökkentené a BDPT képen, de a könyv is megjegyzi, hogy enélkül is jobb eredményt lehet elérni (minőség/sebesség szempontból).

Olyan esetekben, ahol a next event estimation túlságosan lelassítja a programot, ott a BDPT egy nyerő alternatíva (eltekintve attól, hogy MIS nélkül nagyobb a variancia). A konyha jelenetre például (pixelenként 4 pattogás, 4 minta):


Sebesség/szépség arányban a bidirectional path tracing győz, tisztán szépségben a next event estimation, navigálhatóság szempontjából (és sok pattogásra) viszont a naiv path tracing. Feltehető egyébként, hogy én implementáltam szuboptimálisan (előbbit biztos), úgyhogy konkrét mérési adatokat nem mondok (nem is igazán lehet, mert a rajzolás sebessége és a konvergencia gyorsaságának arányát kellene összevetni úgy, hogy egy adott képminőséget elérnek).

Nézzünk inkább bele egy kicsit a kódba (legalább abba a részébe ami nincs kikötve). Az első felmerülő kérdés, hogy a két subpath hogyan legyen eltárolva (egyáltalán el kell-e őket tárolni?). Valójában nem kellene, de akkor még úgy álltam neki, hogy a MIS-t is megcsinálom, ahhoz pedig nem árt, ha megvan a teljes path.

A globális memória értelemszerűen ki van zárva (eleve amiatt lassú minden). Marad a work group local (shared) és a work item local (private) memória. Előbbit már elméletben elhasználtam az anyagtulajdonságokra, úgyhogy nincs igazán választás. Privát memóriába nagyméretű tömböket tárolni viszont rizikós. Számoljunk: GCN architektúrán work item-enként van 4096 temporáris vektorregiszter, az eltárolandó adatstruktúra kb. 6-7 vektorregisztert tölt ki (ha a GLSL fordító rendesen összepakolja). Annyira nem hangzik rosszul (csak ne felejtsd el, hogy ott van a BVH bejárása is, meg minden egyéb dolog).


Mily szerencse, hogy a függvényen kívül deklarált változók globálisan elérhetőek, de mégis a privát regiszterekbe kerülnek (ez sem volt mindig így...). Első lépésként teljesen hasonlóan, mint fent, elő kell állítani a két subpath-ot (azaz pattogunk egyik felületről a másik felületre, a BSDF alapján pedig választunk új irányt). Mivel a MIS-t kikapcsoltam, nem pazarlok időt arra, hogy például hogyan kell a kamera irányra pdf-et számolni (a könyvben megtalálható).

Tegyük fel, hogy a subpath-ok előállítása megtörtént, mi a következő lépés? Fent leírtam: mindent az egyikből megpróbálni összekötni mindennel a másikból (nem, ez nem A három testőr-ből van).


Sejthető, hogy a dolog nehéz része az összekötés. És valóban, rengeteg dolgot figyelembe kell venni (pl. s = 0 implicit path, s = 1 esetén mintavételezni kell egy fényforrást, stb.). Hogy valamilyen elképzelés legyen, az általános esetet mutatom meg (itt külön figyelmet érdemelnek azok a helyzetek, amikor nem szabad összekötni, például mert az egyik BSDF Dirac delta):


A tényleges kapcsolódási pont keresése a GeometryTerm() függvényben van implementálva. Ez hasonlóan a láthatósági teszthez egy any hit jellegű keresés (áteresztő anyagok miatt), viszont nem engedem tovább kísérletezni, mint amennyit a path hossza megenged. Modellezőknek mondom, hogy az áteresztő objektumok lehetőleg egy rétegből álljanak, hogy a rövidebb path-ok is minél jobban hozzájáruljanak az eredményhez.

A MIS hiánya mellett az implementációnak valami problémája van a dielektrikus anyagokkal. Ha belegondolunk ez annyira nem meglepő: hacsak valamelyik subpath nem jutott át sikeresen egy ilyen objektumon, akkor esélytelen normális összeköttetést találni. Ez egyben rámutat a BDPT egy másik igen komoly problémájára: amikor a BSDF szimmetriatulajdonság nem teljesül, akkor azt külön korrigálni kell. Már olyan egyszerű esetekben is megtörténik ez, mint pl. az interpolált normálvektorok. Szintén nem implementáltam le, a megoldáshoz ugyanis kellenek az eredeti (nem interpolált) normálvektorok is, ami csak további helypazarlás. Ezektől eltekintve viszont helyesen működik.

Merthogy ami eddig elhangzott az csak a jéghegy csúcsa. Vannak ugyanis olyan esetek, ahol az eddig bemutatott módszerek elhasalnak. Például amikor a fény csak egy keskeny résen keresztül jut be a jelenetbe (majdnem csukott ajtón). Ennek kapcsán szerettem volna még bemutatni a Metropolis light transport nevű algoritmust, de annyira más szemlélet, hogy külön cikket érdemelne.

Listaszerűen összefoglaltam néhány dolgot, amikkel lehetne még foglalkozni:

rekonstrukciós szűrők: alapvetően a szemcsésedés eltüntetésére (pl. Gauss), de gyorsításra is lehet használni, ha a képet kisebb felbontásban rajzolod és valamilyen szűrővel nagyítod fel a tényleges méretre. Dolgozat: joint bilateral upsampling

gépi tanulás: valamilyen mélytanulásos algoritmust betanítani, hogy a néhány iteráció után előállt zajos képből azonnal előállítsa a zajmentes képet (ez egy igen felkapott téma). Dolgozat: recurrent denoising autoencoder

kvázi-Monte Carlo módszerek: véletlenszámok helyett egy kvázi-véletlenszerű sorozatot használni (pl. Halton-sorozat, Sobol-sorozat, Hammersley-halmaz). A közelítés hibáját lehet velük csökkenteni. Dolgozat: quasi-Monte Carlo

textúra szűrés: mivel a rajzolás nem raszterizációval történik, nem állnak rendelkezésre gradiensek. Dolgozat: LOD strategies

ködösítő közegek: köd, füst, stb. Látványos képeket lehet csinálni (például ködrészecskékről lepattanva kirajzolódik 3D-ben a kausztika). A PBR könyv 11. fejezete foglalkozik ezzel.

Metropolis light transport: az alapötlet az, hogy ha sikerült találni egy útvonalat a fényforrásba, akkor annak mutációiból állítsunk elő újakat. Dolgozat: MLT

ray tracing hardverek: az előny egyértelmű: nem kell külön foglalkozni a metszetkereséssel (így akár nagyságrenddel gyorsabb lehet az implementáció)

Sok szempontból nehéz szülés volt ez, és nem csak a téma nehézsége miatt. Retrospektíven több különálló cikkre kellett volna szabdalnom, mert így az esetleges továbbfejlesztés csak ezt fogja hízlalni.

Végszóként letisztáznék néhány dolgot, amik a ray tracing hardverek megjelenésével pongyolásodtak el. A path tracing (Monte Carlo vagy nem) a ray tracing egy speciális formája. Sajnos amióta elkezdték reklámozni az RTX hardvereket/implementációkat, a két fogalom összemosódott. Ray tracing-nek nevezik, de valójában Monte Carlo alapú path tracer-t implementálnak (pl. WWDC Metal ray tracing).

Miért baj ez: azért mert a "klasszikus" ray tracing nagyjából úgy működik, mint ahogy raszterizációban is csinálnád a dolgokat (kiszámolja a közvetlen megvilágítást, esetleg kiküld egy vagy több shadow ray-t). A globális megvilágítást hasonlóan nehéz vele leimplementálni: minden pattogásnál vaktában kiküld a félgömbön belül újabb sugarakat, és ezt folytatja rekurzívan. Pontos eredményt ad, de iszonyatosan lassú. Ezzel szemben a path tracing-nek konvergálnia kell, viszont mindent ingyen ad, egyszerű leimplementálni és gyors.

Lényeg a lényeg: tudd, hogy mire van szükséged. Ha például csak arra szeretnéd használni az RTX hardvert, hogy árnyékokat generálj, akkor eszedbe ne jusson Monte Carlo algoritmusokkal bajlódni.

Az alábbi tesztjeleneteket innen konvertáltam át saját formátumba (a nagy méretek miatt ezek nincsenek bent a repóban). A konvertert egyelőre nem teszem publikussá, ugyanis a rendereken is lehet látni, hogy nem kezel le mindent (és látszódnak a fent felsorolt implementáltatlan dolgok is, például a rózsaszín nappaliban az üvegcsékben piros ködösítő közeg kéne legyen).

Mindegyik render 256 minta/pixel, legfeljebb 15 pattogással, next event estimation bekapcsolása mellett készült. A gyakorlatban ez azt jelentette, hogy elindítottam az implementációt és kivártam azt a kb. 5 percet amíg erre a minőségre bekonvergált. Mitsuba-ban ugyanilyen paraméterekkel kb. 10 perc, viszont amíg dolgozik nem tudsz mozogni és sosem látod egyben a képet.

Ha már mozgás: természetesen minden beállítás mellett interaktív az implementáció, viszont ~1300 ms frametime (ez volt a leglassabb, amit kimértem) mellett nem igazán van benne köszönet (és persze amint megmozdulok újraindul a konvergencia). A jellegéből adódóan viszont mozgás közben úgy módosítom, ahogy akarom (beleértve akár a temporal convergence ill. disocclusion detection-t is!). Egyszerűbb jelenetek ugyanakkor egész korrekten eldöcögnek ezek nélkül is.

Kód a szokott helyen, néhány videó pedig a másik szokott helyen.


Höfö:

• Csináld meg a textúra szűréseket a fragment shader-ben!
• Implementáld environment map-ek mintavételezését az általános kódban!

Irodalomjegyzék

https://mycourses.aalto.fi/course/view.php?id=20635&section=1 - Advanced Computer Graphics (Jaakko Lehtinen, 2019)
https://www.pbr-book.org/ - Physically Based Rendering From Theory To Implementation (Matt Pharr, 2018)
https://www.gdcvault.com/play/1024478/PBR-Diffuse-Lighting-for-GGX - PBR Diffuse Lighting for GGX (Respawn, 2017)
https://jcgt.org/published/0003/02/03/paper.pdf - Understanding the Masking-Shadowing Function (Eric Heitz, 2014)
https://hal.inria.fr/hal-00996995v1/document - Importance Sampling Microfacet-Based BSDFs (Eric Heitz, 2014)
https://www.reedbeta.com/blog/hows-the-ndf-really-defined/ - How Is The NDF Really Defined? (Nathan Reed, 2013)
https://repository.tudelft.nl/islandora/... - Unbiased physically based rendering on the GPU (Dietger van Antwerpen, 2011)
https://research.nvidia.com/publication/... - Understanding the Efficiency of Ray Traversal on GPUs (ACM, 2009)
http://web.cs.wpi.edu/~emmanuel/courses/... - Monte Carlo Integration: Basic Concepts (Emmanuel Agu, 2007)
https://www.cs.cornell.edu/... - Microfacet Models for Refraction through Rough Surfaces (Bruce Walter, 2007)
https://cg.iit.bme.hu/~szirmay/script.pdf - Monte-Carlo Methods in Global Illumination (László Szirmay-Kalos, 1999)
http://graphics.stanford.edu/papers/... - Robust Monte Carlo Methods for Light Transport Simulation (Eric Veach, 1997)

https://tomacstibor.uni-eszterhazy.hu/tananyagok/Mertekelmelet_eloadas.pdf - Mérték- és integrálelmélet (Tibor Tómács, 2021)
https://tomacstibor.uni-eszterhazy.hu/tananyagok/Valoszinusegszamitas.pdf - Valószínűségszámítás (Tibor Tómács, 2021)
http://www.ksh.hu/statszemle_archive/2012/... - Monte Carlo módszerek a statisztikában (Dániel Kehl, 2012)
https://www.libri.hu/konyv/halmos_paul_r.mertekelmelet-2.html - Mértékelmélet (Paul Halmos R., 2010)